알쏭달쏭 공부한거 쓰기
10월 1일 현대물리 공휴일 대체 강의 본문
Modern Physics_Lecture 5_Atomic Structure
review
-모든 물체가 wave와 particle를 갖고 있는 duality를 설명
- 입자 특성인 모멘텀과, 파장 특성인 wavelength 간의 반비례 관계
-물체를 wave로 표현>matter wave> 여러 서로 다른 wavelength를 더함으로서 표현
>문제점
-모멘텀을 알면 위치 파악x
-wave로 표현시 위치를 알면 모멘텀을 알기 힘듦.
>무언가를 보기전에는 모든 물체가 wave형태로 공간에 퍼져있음으로 위치 파악x할 수 없는 wave형태로 표현되다가
관찰하는 순간 , matter wave collapses되어 입자상태가 된다.
What we studied so far
-Relativity-chapter1
빛의 특성: 개념이 나오게된 이유가 빛의 특성을 만족하기 위해 다양한 물리적 파라미터가 변해야함을 설명하기 위해 나옴
>빛의 성질 개속 연구 : 빛은 전자기파에서 입자일 수도 있음 논쟁이 나옴.
-Particle property of light (chapter2)
-막스플랑크, 아인슈타인이 빛이 입자임을 들여옴
-막스 플랑크: 모든x 정수배의 특정 에너지만 가질 수 있음.
-아인슈타인: photo electric effect를 통해서 실제 의미 파악 :빛은 photon 입자로 이루어, f에 비례한게 에너지를 가
-에너지 양자화
-E=hf
-wave property of electro (chapter3)
-드브로이 확인 개념을 확장: 빛이 wave, particle 특성을 가짐>모든 물체가 그럴것임. >전자도 이중성을 가질것임을 파악
- p=h/λ
-간섭:실제로 증명하는 실험.
-이번에는 how to light and electron ar linked in atomic structre(chapter 4)
:어떻게 관계가 되어있는지 원자 모델를 하나의 예로 배울 것
THIS LECTURE
-원자모델이 어떻게 진행되어 왔는지
-누가 제시했고 제시한 이유(실험)>그에따라 어떤 모델을 제시
-보어 모델
-현대원자모델의 토대
-어떤지
-완벽한 모델은 아니지만, 왜 중요한지 공부
-보어가 제시하는 모델이 에너지 양자화를 실험적 증명함(스펙트럼)
보어 모델.
=행성모델
=양전하를 뜨는 핵이 가운데 전자가 특정 궤도를 도는 형태
>왜 이런 모양이 나왔는지
시작:전자를 발견한 joseph john Thomson 의 실험부터
1897에 전자 파악
Thomson Experiment
>전자를 밝혀냄
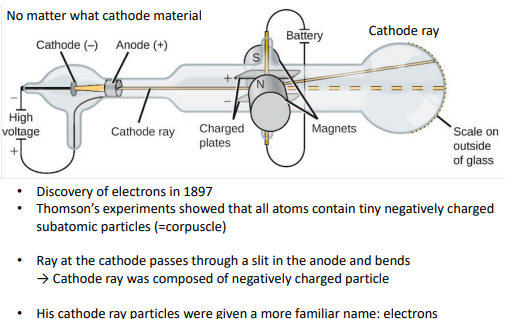
-실험 세팅(어떤 cathode 물질을 사용하든 동일한 결과가 나옴)
-진공공간에서 metal plate에 전압 인가해서 -전압이 인가된 곳 Cathode에서 나온 선을
cathode ray라함.
-anode를 통과한 ray를 분사해서 마그넷을 통과시킴(한쪽 +,- 대전시킨 상태 )
-캐소드 ray가 특정 방향,+로 대전된 쪽으로 bend되어 통과함
결론:cathode ray가 negatively charged particle로 구성되어서 +쪽으로 bend 된 것이다.
>모든 atoms들이 tiny, negatively charged된 어떤 입자로 구성되어 있음.
현대에 와서 cathode ray particles가 전자로 이름 붙여짐.
Thomson Model: Plum Pudding 제시
원자라는건 중성을 만족해야함.
>+로 bend 되었으니 -는 있을거임
>중성을 위해 +입자도 있어야함.
영국에서 유명한 디저트인 plum을 이용해서 tomson model을 제시함.
전자들이 곳곳에 박혀있을것임
중성을 유지하기 위해 양성은 uniformly하게 퍼져있을것임.
+극을 띄고 있는 곳위에 -입자가 수프위에있는것 처럼 떠있다.
Rutherford Gold Foil Experiment
= α particles: two protons and two neutron bound together
이 실험에 의해서 반박되었음.
-무언가를 내보내는 source를 넣음: source에 α particles를 만들어 내는 장치
α particles= two protons(+) and two neutron bound together
>전자 관점에서 총 4개의 입자를 source로 발사, 덩치가 큼.
-Gold 원자로 구성된 foil막에 입자를 쏘아서 어떻게 되는지 살펴봄.
(이당시 foil을 가장 얇게 만들 수 있는 재료였음. 얇았기 때문에 1-3가지 현상이 나타날 수 있었음)
three observation &interpreation
1) 대부분의 α particles은 foil을 통과해서 반대에 도달
> α particles 굉장히 큰 크기인데도(almost 전자 4개이상) 통과했기에 원자 대부분 empty space .
:이전에는 plum푸딩 처럼 꽉차있고 전자가 박혀있는 형태로 있어 빈공간이 없다고 생
2) 몇몇 α particles들은 작은 각도로 꺽임
> α particles이 극성을 띄고 있어 힘을 받음.
중성을 유지하기 위해 +가 골고루 퍼져이씀>> 어떤 +전하를 가진 핵이 존재할거임
3) 경우에 따라 1/20,000의 확률로 α particles이 back from the foil
>+전하를 가진 핵이 원자가 가진 대부분의 질량을 가질거임.
덩치가 큰 α particles이 때렸는데 통과하지 못하고, 핵을 밀지 못했기 때문에 다시 돌아옴
=핵이 dense하고 힘이 세다는것을 의미
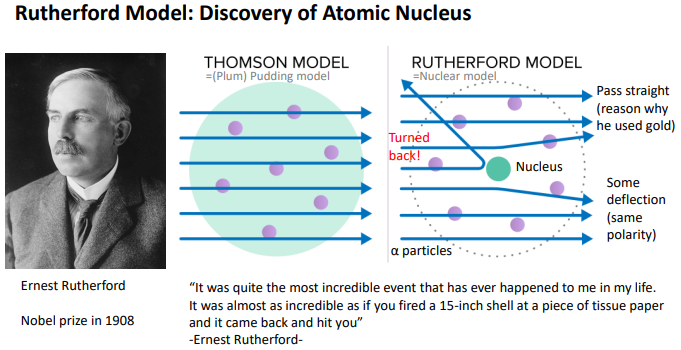
Rutherfod Model: Discovery of Atomic Nucleus
>원자핵의 존재, dense,와 위치를 밝
Thomoson model=plum pudding model
-녹색이 +charged띈 nucleus
-보라색 전자
- α particles를 쏜 방향.
> nucleus가 크니까 α particles가 통과 못할거라 생각했는데 Pass straight를 통해 녹새이 원자모든부분에 존재하진 않는다라고 해석(gold가 가장 얇으니까..)
>+charged인 핵은 중성을 만족하기 위해 반드시 존재해야함. 센터에 있어서 어쩌다가 오는 α particles가 꺽이는걸 설명할 수 있음을 통해 핵의 존재와 위치를 파악
>정확하게 mass가 큰 핵에 있는 쪽으로 α particles가 간다면 통과하지 못하도 다시 돌아올 수 있다.
돌아올 확률이 작기 때문에 핵은 전면적에 퍼져있는게 아니라 어딘가에 dense하게 존재할 것임.
Rutherford Model: Nuclear model
-원자는 매우 작은 +전하인 핵이 센터에 존재하고, -전하인 전자로 둘러싸여서 구성되어있음.
-2)관측에서 α particles이 어떤 angel로 꺽이는 정도로 mass와 density를 파악할 수 있음>핵이 dense하게 가운데 있음
>문제 발생.
what were the electrons doing in the atom?
-전자가 핵에 attractive force가 있는 상황에서 충돌하지 않고 존재할 수 있음?
Rutherford Model: Nuclear Model(=Planetary Model )
러더퍼더: 지구가 달을 당기듯이 중력이 잡아당기는 힘이 아니라는것을 지금에서야 알았지만.
저당시엔 중력은 두 물체가 서로 당기는 힘이라는 개념을 이용해서 설명함.
행성도 서로 attractive force가 있지만 구심력으로 돌기 때문에 충돌하지 않음.
>가운데 핵, 전자가 주변에 도는 원자핵 구조에서 행성 모델이라고도 불림.
Momentum vs Angular Momentum
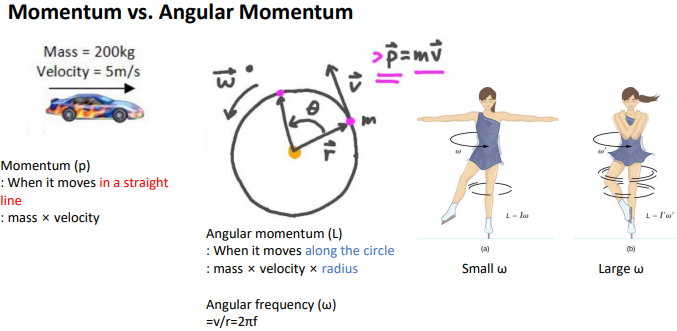
새 개념 도입.
모멘텀: 질량을 가진 물체가 어떤 속도로 움직일때 그 물리량을 표현하기 위해 모멘텀p을 표현함
straight line으로 물체가 움직일 때 운동량을 잘 기술하여 정의한거임.
직선이 아닌 원운동을 한다면 새로운 term으로 정의하자
물체가 circle을 따라서 운동하는 경우에 angular momentum L을 정의함.
Angular momentum (L) :질량*속도*radius(거리)=mvr
Angular frequency (ω) =v/r=2πf
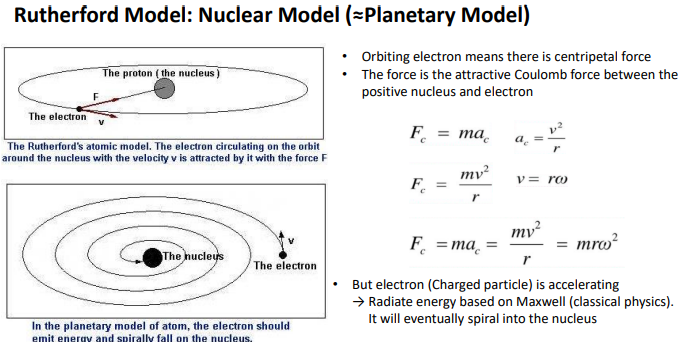
원자모델을 설명하기 위해서 L을 배움.
원자모델을 구심력을 적용하여 해석하려고함.
궤도를 돈다 =구심력이 있다
the proton과 the electron간 구심력이 작용할만 힘.
-coulomb force 다른 극성이 전기적으로 끌리게 된다.
(구심력 )F=ma 원운동의 가속도 a= v^2/r
(속도를 angular freuqnecy로 표현) v=rw
F=ma=mv^2/r=mr ω^2
다른 고전역학에 의해 반박된다.
전자가 원운동을 한다=가속을 한다.
전자는-charged입자가 가속하면> 맥스웰법칙에 의해 주변에 전자기파를 만들어내 에너지를 만들어냄.
>이 전자가 가지고 있는 에너지에서 변형되어 전자기파로 나옴
전자가 돌수록 전자기파가 나와서 에너지가 줄어서 힘이 약해지니까 결국 핵에 충돌해야하는거 아니냐?
이걸 해석하기 위해서 나온게 현대물리학의 Niels Bohr가 해결함.

1)전자가 특정 궤도에서 에너지 손실없이 핵을 돌 수 있을거라 가정
그 이유가 중요
planck constant (h)가 angular momentumd의 unit(dimenstion)을 가짐.
kg x m/s x m= J x s
>전자가 특정 에너지만 가질 수 있음._빛이 정수배의 특정 에너지만 가질 수 있는 에너지 quantization concept를 이용해서 전자도 원자 내의 특정 에너지만 가질 것이라는 concept을 제시함. *
2)플랑크 에너지 양자화 개념
-전자가 fixed, stable(에너지 발산x하지 않고 존재)=non-radiationg states하게 궤도를
각 운동량아 플랑크 상수 배수일때mvr=nh를 만족할 때.
3)아인슈타인의 포톤 개념
-전자가 특정 에너지 상태에만 존재한다면, 그 전자들이 에너지상태를 왔다갔다 할때 그 차이는 f에 비례할 것임.
>다른 state로 jump함. 에너지 차이는 hf
-에너지가 f에 비례하게 가짐
특정한 상태에 있다는 의미, 그 상태가 가지는 의미
>드브로이 이중성을 먼 배운 이유
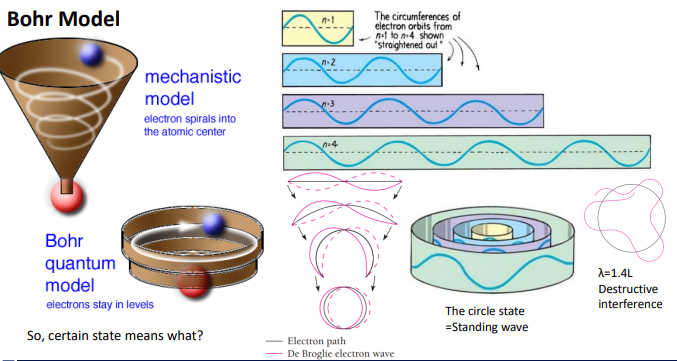
과거 : Rutherford 끌리지 않으려면 돈다> 에너지 발산> 결국, 충돌 :성립x
보어: 모든 영역을 연속적으로 가질 수 있지 않고 전자가 특정 상태에서 돌 수 있고, 특정 에너지만 가질 수 있음
>특정 상태가 가지는 의미!
전자가 특정 반지름을 갖고 원을 도는데, 그걸 쭉 펼치면 오른쪽 그림처럼 된다.
원의 둘레가 2ㅠr
전자가 wave특성을 가짐으로 wave관점에서 봐야함.
어떤 wave만 가질 수 있나? 처음과 끝이 boundary condition이 맞아 떨어지는 (1 lambda)
왜냐하면 다시 원으로 붙였을때 wave의 모양을 설명하면, wave 끝이 연결되기 되기에 연속적으로 이어질 수 있음.
if wave가 도는데 wave length가 처음과 끝이 맞지 않았더라면, 결국 간섭이 발생해서 상쇄간섭 발생으로
결국에는 아무로 wave가 보이질 않을 것임.
>phase가 동일/ 처음 끝가 동일한 wave만 원으로 이었을때 끊기지 않고 연속적으로 연결되어 살아남을 수 있음.
이 wave를 standing wave라고 한다. =정상파, constructive 보강 간섭을 만들 수 있는 상태
모든 파장이 이 에너지 상태에 존재할 수 있는게 아니라 이 길이에 맞는 특정 파장길이를 갖는 파장만 존재할 수 있음.
이 개념을 이용해서 수식으로 살펴봄.

전자가 돌면서 에너지를 잃지 않고 돌면서 해당 궤도에 존재할 수 있는지 수식적으로 설명 * 시험 나올것 같아.. 과연
-구심력=쿨롱힘. k상수
-전자의 관점에서 에너지=키네틱(move)+포텐셜(attractive)
-PE=U
-뭐에 반비례, 비례한지 보면 됨.
>에너지의 term이 거리에 반비례, 전하의 제곱에 비례
중요한 concept 2가지
1)음수를 띄고 있음> 전자는 bound되어 있다 by positive charge
*2)에너지가 모든 거리에 대해 모든 에너지를 가질 수 있는걸로 표현된다.
>엥?그럼 양자화 아니자노? 도입하자
INTRODUCE QUNATIZATION

도입 2가지가 있음
첫번
보어- 각운동과 플랑크 상수의 단위가 동일에서 시작
-L=nh(h는 모든 에너지가 아니라 정수배 에너지만 가짐)
-h바:상수들을 하나로 묶어서 식을 간단하게 하기 위해서 도입.
-속도로 정리:n에 해당하는 특정 거리, 특정 속도만 가질 수 있게 됨
-KE:1/2mv^2에 v대입
-KE를 각운동량이 양자화되어 있음은 왼쪽 항으로 구심력과 쿨롱힘으로 표시한것을 오른쪽 항으로 둠
-거리 또한 양자화됨을 알 수 있음.
-n외의 나머지 다 상수인데 a0로 표현가능
n=1일때 Bohr radius라고 정의
r1=a0>상수
rn=n^2a0
거리가 a0의 n^2에 비례하게 나타남.
특정 값만 가질 수 있음.
2번째
드브로이 아이디어 - 원심력=쿨롱힘에서 시작함.
-v로 정리
-입자라고 알려진 전자가 파장 특성을 가짐으로서 , 플랑크 상수로서 반비례 관계를 가짐.
- λ(람다, 파동) = h(프랑크 상수) / p(운동량=mv)> λ로 정리
여기서 양자화 term을 넣어야함.
-드브로이는 전자가 도는 궤도 원의 둘레를 펼치면 λ에 비례하는=phase가 같은 형태만 가져야함.
2ㅠr 원의 둘레가 λ의 배수만 가질 수 있게해서 양자화 시킴. -nλ=원의 둘레> r정리함. -상수부분처리, a0정리하면 위와 동일할게 나옴.
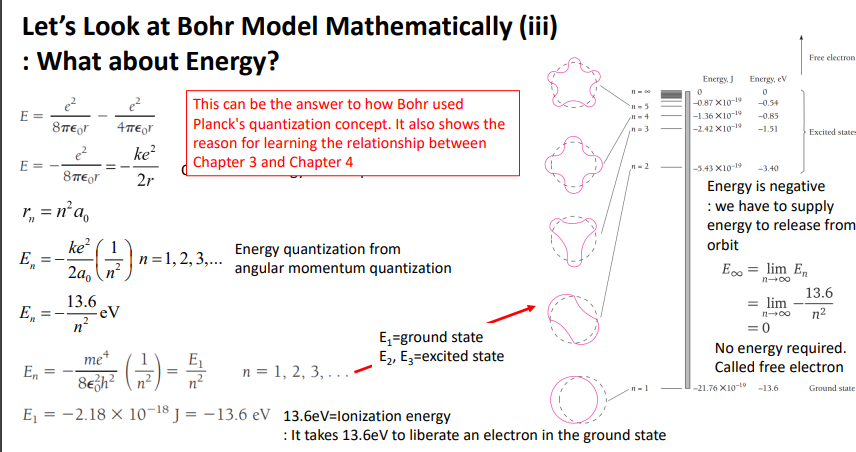
과거의 문제
에너지가 pe+ke로 표현시 묶여있는데 모든 r에 대해 연속적인 에너지를 가지는게 문제
도입 방법
2가지의 서로다른 양자화방법을 통해 r이 특정 값만 가질 수 있도록함.
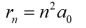
을 대입.
에너지는 연속이 아닌 rn에 해당하는 특정 거리에 대한 (discrete)특정 에너지만을 가지게 됨.
상수 대입해서 정리하면
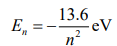
이렇게 나옴.
k를 다 풀어쓰면 아래와같은 식이 나옴.
n=1일때 에너지를 구해서 대입하면 위와 같은 식.
n에대한 식으로만 에너지를 표현할 수 있음.
E1=-13.6 eV으로 묶여있는 상태
에너지가 가장 낮은 상태 , 자연은 항상 낮은 상태가 됨.
대부분 E1에 존재, 대부분 묶여있음으로 ground state
E2=더 높은 값이 됨.=에너지는 높은 상태-3.4
에너지가 높은 상태라해서 excited state가 된다.
상태를 구분함.
-13.6은 전자가 묶인 에너지
H원자 핵1개에 전자1개인 원자는 13.6ev를 가지고 묶여있는 상태
외부에서 13.6ev를 인가시 전자가 탈출하기에 충분한 힘이 되어 빠지게 됨.
중성을 유지하던 원자가 전자가 빠지면서 +인 핵만 남아 이온이 된다.
13.6eV를 ionization energy라고 함. =ground state에서 전자를 자유롭게하는데 필요한 에너지
-에너지를 가한다?
음수이기에 묶여있음으로 에너지를 외부에서 supply해야 oribit에서 release할 수 있음.
-E무한대

n이 커지면 에너지가 0으로 감.
굉장히 높은 상태
전자를 궤도에서 빼낼 때 에너지를 인가해야하는데 묶인에너지가 0이니까 에너지를 주지 않고
쉽게 나갈 수 있음=free electron
이런과정이 보어가 양자화 과정을 이용한 답이 됨.
이런 이유로 원자 구조를 다루기 전에 드브로이의 입자 파장 특성 이중성을 배운 이유임. (전자가 wave특성을 가짐)
>전자가 특정 에너지만을 가질 수 있음.
chap3,4의 관계
여기까지가___플랑크가 제시한 양자화 개념을 다룸
아인슈타인의 양자화 컨셉을 도입.
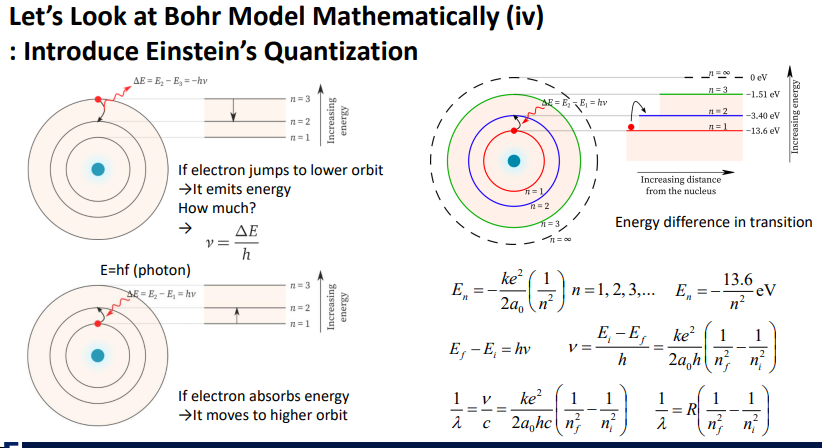
에너지=검은선=하나의 궤도
연속이 아니라 특정 상태만 가짐을 나타냄.
전자가 움직이면 n=3 에너지가 높은 불안정한 상태
에너지가 낮은 상태로 간다면, 가지고 있는 많은 에너지를 빛의 형태로 내보냄.
얼만큼? 에너지 수식 에너지는 주파수에 비례해서 그만큼만 내보냄.
여기에서 에너지의 차이를 얼마인지 알려면 주파수를 확인하면 된다.
에너지를 받으면, 전자는 더 높은 궤도로 감.
n=1과 n=2의 차이만큼만의 에너지를 받아야 (photon) 다른 state로 감.
-photo electric plate에서 배운 어떤 plate에 빛을 인가했을 때 전자가 반대 plate에 도달할 수 있는 이유는
이 plate에서 원자가 구성하고 있는 work function을 깨고 초과된 에너지가 KE로 바뀌었기 때문에 반대 plate에 도달 할 수 있었음. 그래서 전류가 흐름
-왼쪽 아래 그림은 photo electric plate를 보여주는 그림.
-왼쪽 위 그림 photo electric plate개념과 반대되는 x-ray개념을 설명함.
열을 가해서 전자를 가속시켜 plate에 때리면 빛이 나옴.
빛의 파장이 x-ray영역이라서 우리가 활용함.
x-ray는 원자 구조 내에서 가속전자가 원자의 궤도의 전자를 치고 빠지면서 빈자리가 생김.
더 높은 상태의 전자가 빈자리를 채우면서 에너지를 빛의 형태로 냄.
몇번째 shell ,step에 따라 이름이 다른 그 concpet을 나타냄.
에너지간의 transistion은 수식으로 설명된다.
에너지가 가지는 값을 앎
에너지의 차이는 주파수에 비례
나중과 처음 상태를 안다면, 주파수를 알 수 있음.
-자체적으로 음수였음으로 중간 처음-나중으로 바뀜
-몇번째의 궤도인지가 중요 나머지는 다 상수로 계산
-빛을 볼때는 주파수 보다는 파장길이를 보니까 파장길이로 정리
-nf,ni로 파장길이를 계산할 수 있음.
이렇게 제안한 것을 실험적 증거로 스페트럼에 이용할 수 있음.
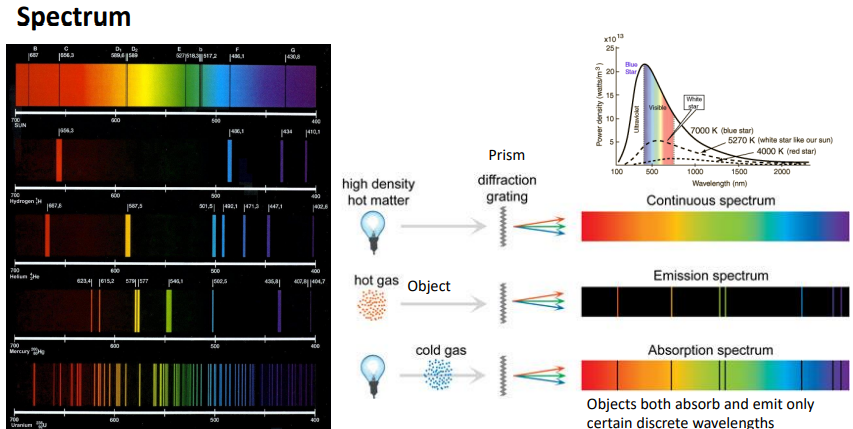
-가까워지면 파장길이가 어디로 가는지..멀어지면 어디로 가는지 도플러 효과로 >우주가 팽창하고 있음을 밝힌 스펙트럼
-컬러들이 어떻게 나올 수 있는지
1)모든 파장의 빛이 연속적 -balck body, sun,white light
2) 어떤 object인 경우 특정 파장대만 방출하는 경우가 있음.>검은색에 해당하는 파장길이는 가지지 않음.
3)모든 빛을 내는 것 앞에 물체를 넣으면 연속적인 스펙트럼에서 검은색 line이 생김= 특정 peak만 존재하지 않음.
특정 물체가 해당 파장길이의 빛을 흡수했기에 내보내지 못하고 걸러져서 안보이는거임.
왼쪽 그림: 예시
-태양 일반적으로 모든 빛을 낸다고 알려져 있지만, 태양 앞에서 수많은 gas들이 있어서 검은 line을 통해 분석할 수 있음.
수소,.헬륨 등 개별적으로 자발적으로 나타내는 방출 스펙트럼을 토대로 흡수 스펙트럼을 분석하면(missing point)
태양앞에 어떤 종류의 gas가 있는지 분석할 수 있음.
수소 스펙트럼과 일치함으로 태양에 수소가 있음을 알 수 있음.
또한, 헬륨의 pick과 일치 헬륨도 존재
이 스펙트럼을 이야기하는 이유
>스펙트럼을 기반으로 보어 모델이 강하게 confirm
-수소 스펙트럼
white light + 수소 +prism> 흡수 스펙트럼 특정 파장만 없는 스펙트럼.
excited 수소 +prism >방출 스펙트럼. 특정 파장만 가진 스펙트럼
how this 보어 모델 컨펌
-수소가 흡수하고 방출하는 파장의 길이를 어디서 기록되었는지 계산
아인슈타인 양자화 개념을 하면서 에너지는 주파수에 비례하게 가짐, 에너지 차이도 주파수로 표현 가능
final state와 inital state로 파장길이를 알 수 있음.
흡수 스펙트럼에서 missing point에서 실험적으로 알 수 있고
두개를 matching시키 확인
>해당 주파수에서 흡수된게 맞음.
실제로 원자가 궤도를 가지고 에너지를 얻고 방출해 움직임을 스펙트럼으로 실험적 증거가 됨.
-n2에서 n3로 이동하는데 656.47nm만큼의 파장길이인 주파수가 필요로 함.
실제로 스펙트럼에서 흡수된 주파수와 동일
white light을 쏘면, 수소에 파장 중 656.47을 가진 빛이 들어오면 n2>n3으로 가기에 충분한 에너지기에 흡수에서
excition되는 과정이 있어 빛이 흡수되어 검은색 라인으로 나타나 눈에 보이지 않게 됨.
-보어의 원자 모델처럼 궤도가 존재하고, 연속적이지 않는 특정 궤도만을 가지고 있음을 support
-그때의 상태가 정수배에 비례한게 아니라 n에 제곱에 비례
>각운동이 플랑크 상수의 단위와 동일
>드브로이의 파장 개념을 이용했을 원을 펼쳤을때 원의 둘레가 nλ에 비례해서 계산.
이걸 적용해서 계산한 에너지가 실험적 에너지 값과 동일하다는 결론이 나와서
보어모델이 인정받게 됨.
앞에서 몇 번째 궤도인지만 알면 방출하는 파장을 알 수 있으니, 해당 파장만을 가지고 있다?
양자화된 궤도임을 나타내는 실험적 증거임을 설명함.
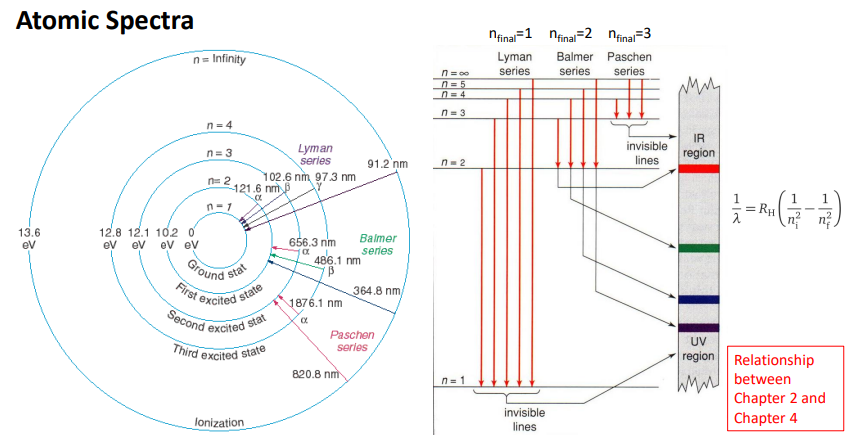
정리
-각가의 에너지 값이 n 정수배라는 의미
1-4이든 플랑크가 제시해서 정수배로 가진다는것을 알게됨.
E 13.6, 12.8..등등 왜 구체적인 수치가 나오게 되었는지가 더 중요함.
2가지 양자화 개념이 도입이 되어서야 E 구체적인 값이 계산되었음.
13.6이기 때문에 앞에서 수소 흡수 스펙트럼의 파장이 맞아떨어졌던것임.
보어모델로
-특정 궤도만 가짐.
-특정궤도에서 에너지를 잃지 않고 항상 stable하게 standing wave형태로 돌면서 존재함.
-궤도를 움직일 수 있는데, 움직일때 에너지 차이만큼 주파수에 해당하는 빛을 흡수, 방출 하면서 움직일 수 있고
-이것을 실험적으로 스펙트럼 라인을 통해서 파악함.
어디서 시작이 되든 결국 final point가 다 1인 경우에는 Lyman series라고 부름
nfinal=2인경우 Bairrer series라고 부름
- 각각의 에너지 차이를 알고 있으니> 수식에 의해서 파장을 알고 어디에 찍히는지 알 수 있음.
IR:long
UV:short, f큼, energy큼
=선과 선의 차이= 에너지차이
-uv가 나올려면 nfinal=1이어야 나옴.
-blue LED가 나오게 하려면 파란 파장이 나오도록 설계
-IR파장이 필요하면 최대한 nfinal =3보다 떨어지지 않게 만들어야함.
해당 내용으로 알 수 있는 것.
cha2 아인슈타인의 photo electric effect 양자화 개념과 cha4원자 모델의 관계를 볼 수 있었음
'3-2학기 > 현대물리' 카테고리의 다른 글
| 현대물리 시험 정보 (0) | 2024.10.15 |
|---|---|
| 10월 3일 현대물리 (공휴일 비대면 강의) (2) | 2024.10.05 |
| 9/24 현대물리 (0) | 2024.09.26 |
| 9/19일 현대물리 (1) | 2024.09.19 |
| 9월 12일 현대물리 lms강의(conference) (4) | 2024.09.19 |



