알쏭달쏭 공부한거 쓰기
9월 12일 현대물리 lms강의(conference) 본문
-
review
중력: 당기는 힘이 아님.
아인슈타인 일반 상대성 이론을 정리해보자면
“Spacetime tells matter how to move; matter tells spacetime how to curve” -John Archibald Wheeler -
ex)사과가 떨어지는 것은 시공간의 변화에 따라 물체가 변하는 것임.
사과의 시공간이 아래쪽으로 curved되어 있음> 가지에 매달린 힘이 부족하면 아래로 가는거임.
시공간 변화>물체의 변화> 시공간 변화를 물체의 이동으로 인지할 수 있음.
>중력을 시각화
상대성이론 2가지
-특수 상대성 -일반 상대성
등속운동일때 특수
가속하는 경우 일반
>extension
상대성을 통해서 time, mass, legth,..등등이 달라짐 특수(빛과 관련)
중력과 관련된 상대성(일반 상대성)
이번 시간 강의
빛에 대한 이해
1.빛의 Wave property,
맥스웰 방정식>wave eq
2.빛이 입자여야 설명되는 3가지
-black body raiation
-photoelectric effect
-compton effect
3.planck 상수의 의미. h
-empirical constant 실험적 상수
E=hv 상수*frequency> 입자여야 설명되는 수식
outline(topic connection)
1.상대성(중력,시간,질량 바뀜 빛의 속도가 일정하기 위해서)
2. 빛에 관심> quantummechanics
3. 빛을 이해한 개념을 물체에 적용할 수 있음>전자의 이동에 이해
뉴턴
-빛=입자
-입자임을 설명할 수 없는 빛 물리적 특성= interference> 빛은 파동임(이중 간섭실험)
맥스웰
-빛=파동
-맥스웰 법칙-전자장-자기장 연관
-파동방적식(전자기장-빛 연관)
3가지 효과> 빛=입자
-blackbody radiation(현대물리 탄생)
-photoelectric effect(아이슈타인 상받은 부분)
-compton effect(산란)
빛?
왜 배움.
하늘은 왜 파랗고.
해가 질 때는 왜 빨갈까
1. 하늘이 파란 이유 (레이리 산란, Rayleigh Scattering)
태양빛은 여러 파장의 빛으로 구성된 백색광입니다. 백색광은 가시광선 스펙트럼에서 다양한 색을 나타내며, 각 색은 서로 다른 파장을 가지고 있습니다. 전자기파로서 빛은 공기 중에서 입자들과 상호작용하면서 산란되는데, 이때 산란 정도는 빛의 파장에 따라 다릅니다.
- 빛의 파장은 보라색, 파란색이 짧고, 빨간색, 주황색은 더 깁니다.
- 레이리 산란은 파장이 짧은 빛일수록 더 많이 산란되는 현상입니다. 이 때문에 태양빛이 대기 중의 공기 분자들과 상호작용할 때, 짧은 파장을 가진 파란색(약 450nm) 빛이 다른 색보다 더 많이 산란됩니다.
- 실제로 보라색 빛도 산란되지만, 인간의 눈은 파란색에 더 민감하기 때문에 하늘은 파랗게 보입니다.
2. 해질녘 하늘이 붉은 이유
해가 질 때 하늘이 붉은 이유는 태양빛이 지구의 대기를 더 길게 통과하기 때문입니다.
- 태양이 수평선 근처에 있을 때, 태양빛이 대기를 통과하는 경로가 더 길어집니다.
- 긴 경로를 지나면서 짧은 파장의 빛(파란색, 보라색)은 대기 중의 분자와 입자들에 의해 거의 모두 산란되어 없어집니다.
- 남은 것은 상대적으로 산란이 덜 되는 긴 파장의 빛인 빨간색과 주황색입니다. 이 빛이 우리 눈에 도달하면서 하늘이 붉게 보입니다.
이 현상은 전자기파의 파장에 따른 산란의 차이로 설명됩니다.
뉴턴의 아이디어
프리즘실험으로 가시광선이 나타남.
프리즘을 두개 놓고 실험.
빛-초미세 입자의 집합이라 생각함.
1.그림자. (빛 통과x)
2.굴절(rainbow색으로 분리-white light is mixed rays)- red light heavy mass> 덜 굴절 refracted
3.반사(굴절률이 다른 매질meium 통과시 각도차이 생김)
입자로 잘 설명된다
>light is particle principia
그러나 1가지가 설명이 되지 않음.
Interference 간섭
Huygen's principle
incident plane wave(입사 평면파) 들어와서 하나의 slit 구멍을 만나면 point source로 작용해서 원형 방사로 퍼진다.
slit이 2개라면?
Double-slit experiment
파형이 두개의 구멍을 만나면, 파동의 모습이 어두운색과 밝은색이 patterns을 가져서 나타남.
why: 각가의 point source로 생성된 원형파형이 겹치면서 phase가 겹치는 영역이 상쇄, 보강 간섭이 나타나 색이 달라져 보임.
>빛이 wave여야 설명이 된다.

Maxwell's eq
4가지 수식 의미
전기장과 자기장의 연관성 의미
원인과 결과를 수학적으로 나타냄
q가 발산방향으로 전기장E을 만들어낸다. area에서 발산형태를 띄고 있음.
-면적에 대해서 Q가 E를 만들어내는 관계가 있음.
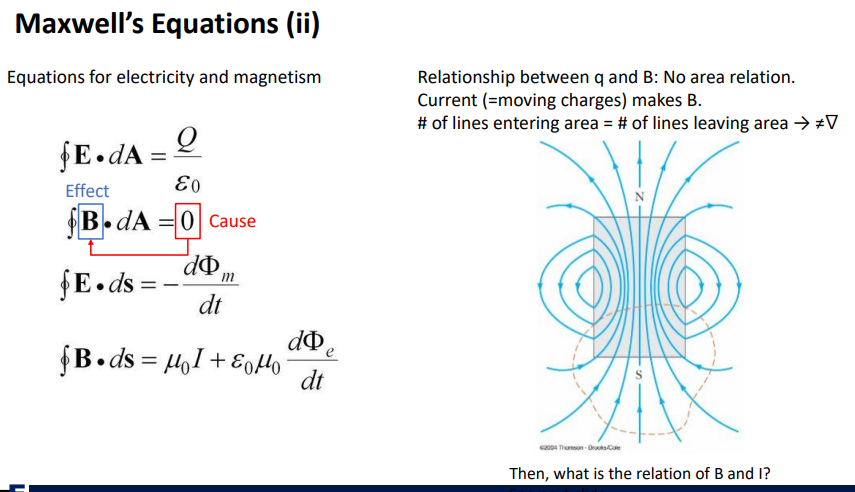
원인 0, effect B
-자기장과 면적과 관계가 없음.
>B field를 만들어내는 건 전류이기 때문에 면적과 관계 없음.
q가 면적에서 내보내기만하는 전기장과 달리
자기장은 나갔다가 다시 돌아오기 때문에 알짜는 없음.
즉,발산이 아님.
>그럼 어떤 관계가 있음? 패러데이 법칙
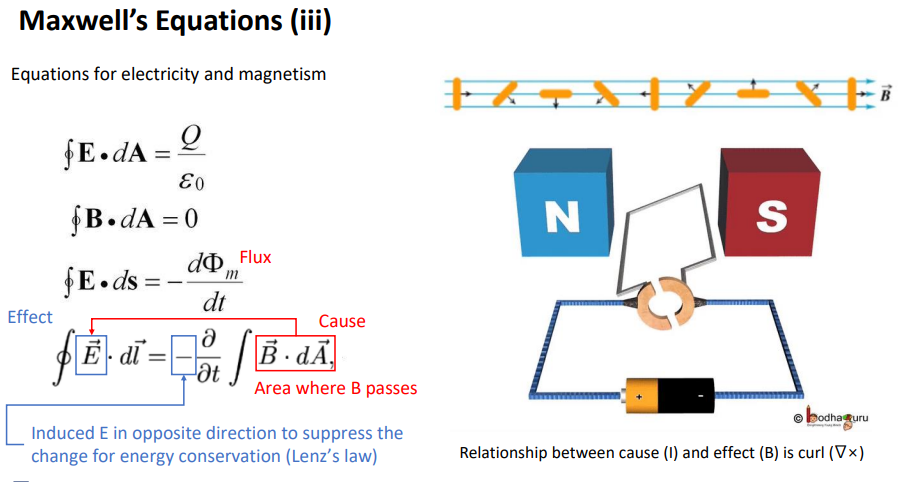
패러데이 법칙
원인: B filed를 통해서 E field가 만들어짐. line과의 음수관계가 있음.
E를 만들어내는 건 에너지 보존 법칙에 의해 자연의 억제하는 방향으로 음수가 붙음.
에너지 보존법칙이 자연계를 설명.
원인: B가 통과하는 면적을 다르게 하면 > E가 만들어짐.
90일때 제일 max면적
0일때 0
>반복되면 E를 만들어냄.
B는 I 는 curl의 형태의(line) 관계를 가짐
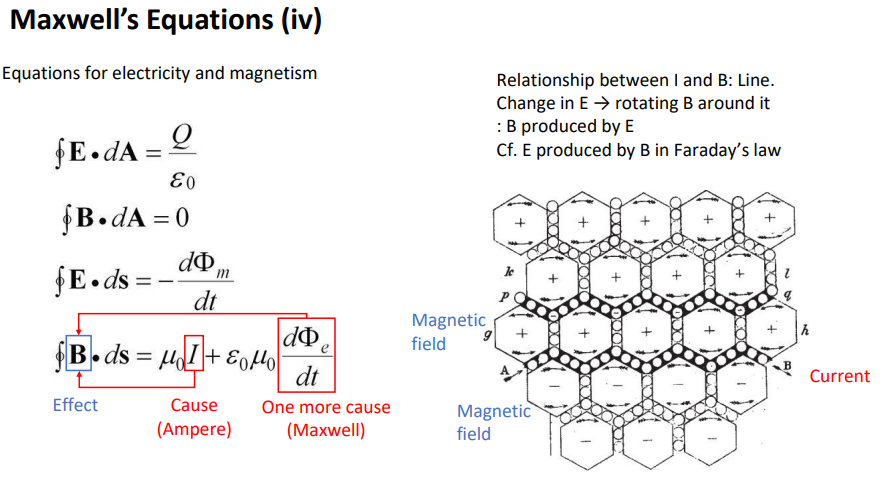
3번째 수D 필드가 E필드를 유발한다.
4번째>그럼 E필드의 변화가 D필드도 만들것이다.
전류> B < 새 원인. 떨어진 전류의 영역에서도 B필드 흐를 수 있음. (맥스웰 한 개 더 추가)-displacement current
원인2개-B 필드
수식을 정리한 이유> wave eq에 넣기 위해서.
끈, 라디오 wave의 움직움을 설명, 묘사할 수 있음.( 수면파, 소리, 빛... etc)

-u=파라미터(수면파, 전자기파..)
시간에 대해 두 번 미분
역삼각형=공간에 대한 미분(dx,dy..)
왼쪽-시간에 두번 미분
오른쪽- 공간에 두번 미분
한 식이 빛 속도의 ^2 만큼의 관계가 있다.

맥스웰 eq을 wave eq에 대입
이렇게 해석될 수 있는걸 단순 적용할 수 있게 만들기 위해 curl적용
curl B 수식 적용
p/E 는 x,y,z가 아닌 상수이므로 공간에 대한 미분시 0으로 된다.
B 수식 대입시 1/c^2은 e0u0로 이용해서 수식 전개
free space 아무것도 흐르지 않는 떨어진 공간> 단위시간당 흐르는 전류가 없음 .
수식 두 항만 존재.
공간에 대한 dx수식으로 정리시 wave eq수식 폼을 따라간다.
>어떤 파라미터에 대해서 공간으로 두번 미분한 항은 시간에 의한 두번 미분한 항은 1/v^2만큼의 관계가 있음
>따라서 전자장이 wave임을 알 수 있음.
>u0e0가 빛의 속도와 관련이 있음.
>전기장=wave=빛의 속도 =빛
마그네틱 필드로 전개시 wave eq과 동일한 식이 전개된다.
>B=wave=wave속도는 빛의 속도= B도 빛
전기장>자기장 유발>전자기장>그 wave가 빛임
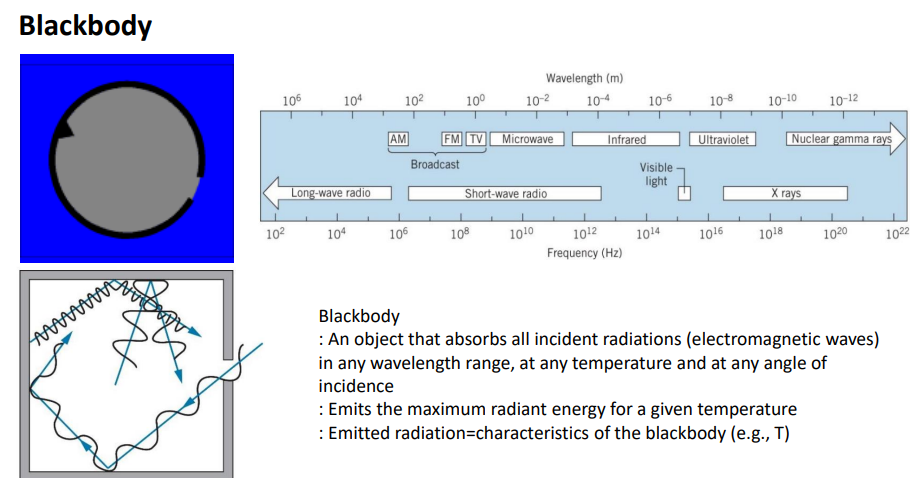
문제 발생
빛이 wave로만 설명되지 않는 문제가 생김
-Black body
모든 빛을 흡수하는 물체
-any wavelength
-any temperature = 분자들의 평균 운동에너지 =모든 에너지 흡수
-any angle
-주어진 에너지에서 최대의 빛 에너지를 방출한다.
-방출하는 빛=blackbody의 특성들을 가지고 있음.
blackbody 안을 보지 않아도 나오는 빛을 보면 물체의 특성을 알 수 있음.
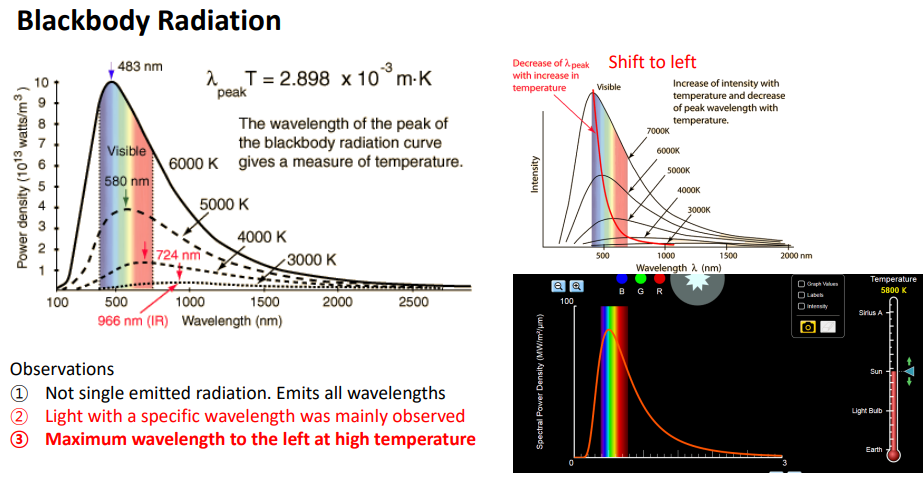
blackbody가 내보내는 빛을 조사시 알 수 있는 특징
-여러 wavelength의 모든 빛이 방출된다.
-그중 특정한 파장이 주로 관측
-온도가 높을수록=평균운동에너지가 클수록>최대파장이 왼쪽으로
왜 중요함?
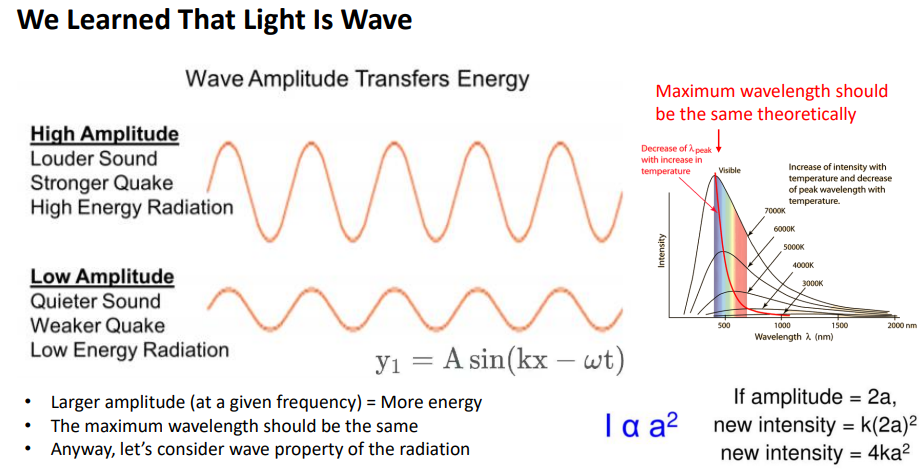
빛이 wave라는 것을 알게 됨.
온도가 올라감=운동에너지가 큼= wave에서는 amplitude증가 (주파수 고정)
>온도가 올라가도 최대파장은 동일한채 intensity만 올라야함>>근데 다르게 나옴.
일단 빛이 wave로 가정한채로 계산
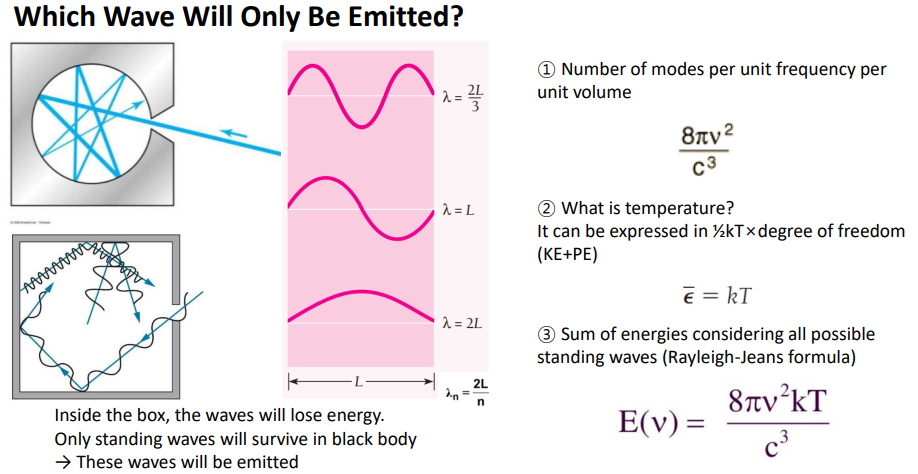
blackbody-모든 빛을 흡수하고 어쩌다 나온 빛이 그 특성 반영
빛은 언제 어떤 파장으로 나오는가?
안에서는 내부에서 충돌하면서 에너지를 잃을것임.> 여러 wave가 충돌하면서 간섭이 발생해서 페이즈가 맞으면 보강, 다르면 상쇄 간섭이 일어남.> 눈에 보이는건 살아남은 보강 간섭만 남음
>수학적으로 표현하면 박스의 길이를 L이라고 하면
경계가 끝이 0일때만 살아남음 x=0,x=L 일때 끝이 상쇄 간섭이 일어나지 않게 되는 파동의 모습이 정상파가 살아남음.
파장이 2.1L인 경우에는 벽에 부딪혀 다시 오면서 페이즈가 달라져 상쇄 간섭이 일어나 제거됨.
>정상파 2L/n n에 비례하게 살아남음
물전
-어떤 파장 빛이 존새시 얼만큼의 state가 존재하는가
-각 state에 얼만큼의 에너지가 필요한가.
-DOE 각 state의 얼마의 확률로 채워져 있는지
동일하게
blackbody박스 안에
-얼만큼의 상태가modes가 존재하는지 (단위 부피당 특정 주파수에서)-박스안에 몇개의 상태가 있는지
-그 상태가 가지는 에너지> 온도=평균 운동에너지로 측정 열에너지 1/2kT x degree of freedom(2)> e=kT
degree of freedom(자유도):wave들이 kT들 열에너지를 가지고 있는 어떤 에너지로 바뀔 수 있는 표현.
total E=KE+PE
-가질 수 있는 가능한 정상파 에너지들의 총 에너지 평균 =상태*에너지
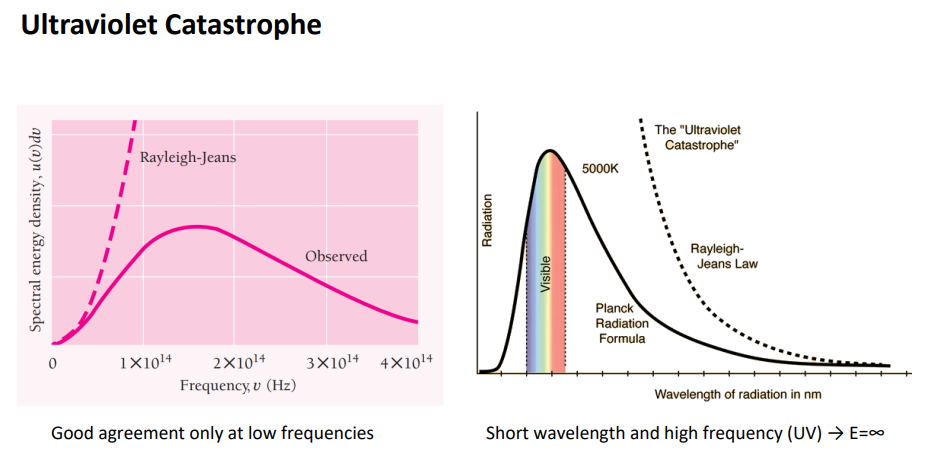
rayleigh-jeans가 제안한 수식
빛이 wave라고 하면 주파수가 낮을 부분에서는 잘 plat된다 그러나(핑크색 왼쪽, 흰색 오른쪽)
blackbody핵심-최대 파장이있고 다시 감소
>최대파장이 존재하고 감소하는 부분을 설명하지 못함. 이론대로라면 계속 증가해야함.
>wavelength가 작은 영역에서 설명이 안된다.

설명되지 않는 부분을 해결하기 위해>막스 플랑
1) 이만큼의 갯수를 가짐>동일
2) blackbody에서 나가는 빛이 모든 에너을 가지지 않는다.
레일리- 모든 에너지가 평균으로 표현>kT
플랑크-모든x discrete에너지=quanta 셀 수 있는 갯수만 나타남
>양자역학의 시작. 훗날 아인슈타인이 quantum of light 증명
에너지를 가질수 있는 state 수는 동일
가지는 에너지가 kT가 아닌 다른 수식>의미x 수학적 fitting을 위해 만듦
hv(주파수) term가짐
Planck's radiant formula 갯수x에너지 (중요x)
수식이 가지는 배경의미 알기: 모든 에너지 평균한 것이 아니라 에너지가 특정 값을 가진다고 제안이 중요
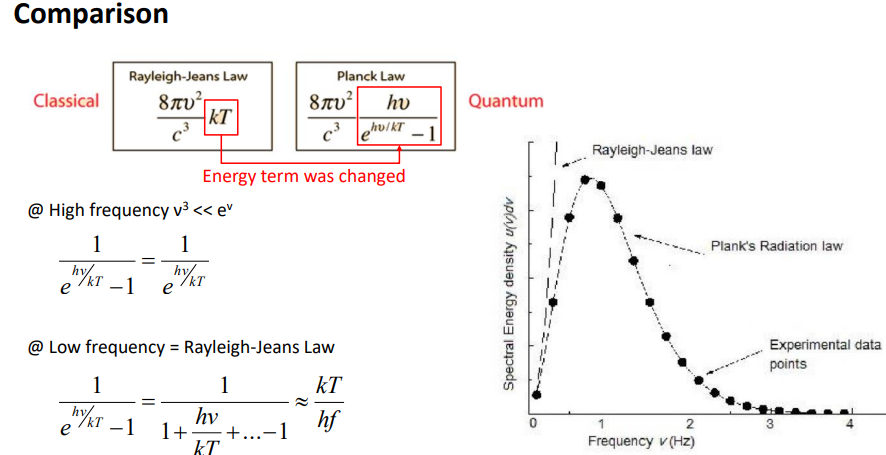
레일리(classical)-kT
플랑크-discrete 에너지
둘의 차이: 에너지 term
의미파악>왜 exp term과 주파수 term을 넣은 이유
-실험적으로 x축 주파수가 높은(바른) 구간에서 맞지 않음
-레일리에서는 주파수^3이니까 최대 파장 찍고 내려오지 않음 하지만 실제로 관측결과에서는 떨어짐.
주파수가 증가할떄 에너지가 떨어지게 하기 위해 exp term추가
주파수가 커져도 v^3<<e^v가 더빠름 분모가 dominant해져서 sum energy가 감소를 표현
이론이 주파수 작을때와 클때 모두 만족하게 하기 위해서
주파수 작을 때> e^a -1= 1+a -1로 나타낼 수 있음. > 주파수가 작을 때는 레일리 수식가 같아지도록 분자에 hv를 넣어둠.
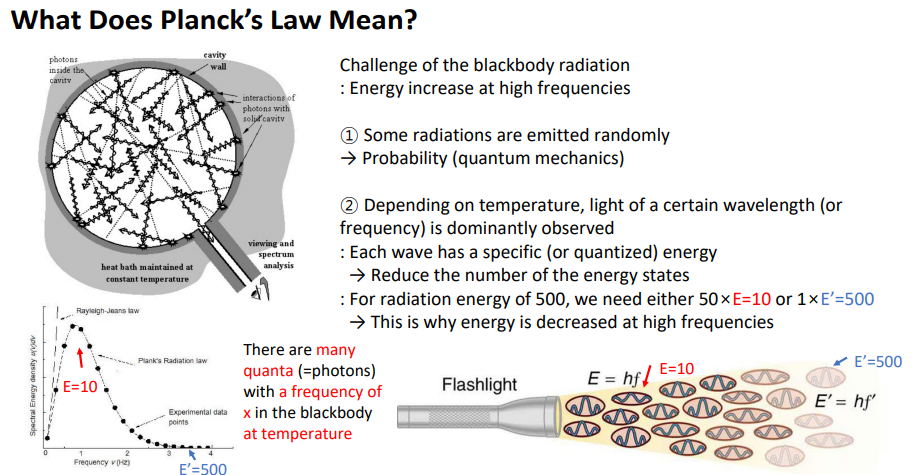
플랑크 수식의 실제 의미
blackbody 빛의 문제점= 주파수가 높을때 에너지가 증가 (실제로는 감소)
1)some 빛들만 랜덤하게 관측
-모든 파장이 나오는데 특정 파장만 많이 나옴.> 확률 개념이 나옴( quantum 역학 기술x지만 확률 개념이 시작)
2)온도에 따라 특정 파장이 나오는데 >왼쪽으로 움직임
sol> total E= modes*energy
kT> 에너지 갯수 줄임(quantized)특정 값만 갖는다고 정의 > 에너지 state가 감소> 레일리와 반대로 감소함.
플랑크가 에너지를 구분 지어었지 지빛이 particle이라 설명x(입자 단어는 아이슈타인이 시작)
뉴턴(입자)>wave> 입자(블랙바디 설명)
빛=알갱이로 정의 =photons= quanta
500E가 나왔다면, E=10이 50개>나올 확률이 많아서 에너지 500이 나타낼때 e=10이 주로 관측되는 것
E=500=1개..?>나올 확률이 굉장히 작음> blackbody에서 나오긴 하지만 intenstiy가 굉장히 작다.
(아인슈타인이 설명)
다음시간에 E가 F에 비례
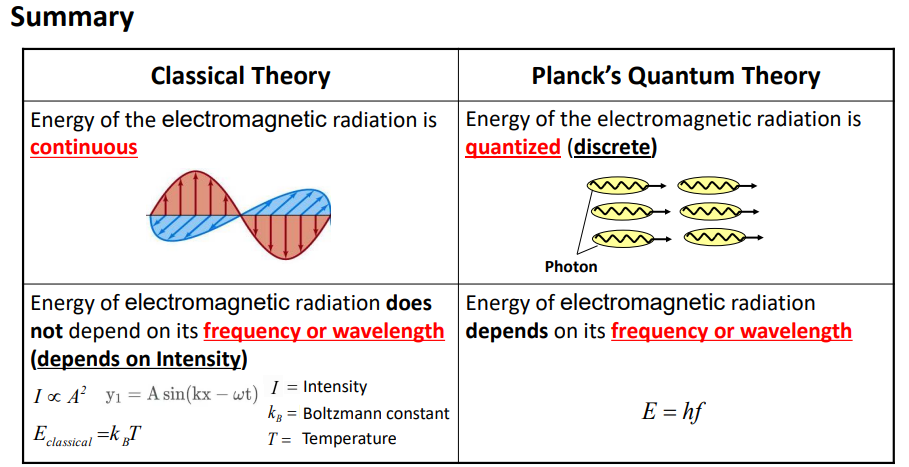
연속> 에너지>평균>크기 amp
불연속> f의존
'3-2학기 > 현대물리' 카테고리의 다른 글
| 10월 3일 현대물리 (공휴일 비대면 강의) (2) | 2024.10.05 |
|---|---|
| 10월 1일 현대물리 공휴일 대체 강의 (0) | 2024.10.04 |
| 9/24 현대물리 (0) | 2024.09.26 |
| 9/19일 현대물리 (1) | 2024.09.19 |
| 9월 10일 현대물리 lms강의(교수님 conference) (0) | 2024.09.19 |




