알쏭달쏭 공부한거 쓰기
9/24전자회로설계 본문
Stability & Frequency Compensation
3장 feedback과 연결
피드백 장점
이득 둔감, 대역폭 증가, 입출력 ideal하게 조정
피드백 단점
이득 둔감(1+베타A)만큼 나눔 손해>장점을 얻어냄 대역폭
결정적 단점:베타도 주파수에 바뀔 수 있는데 계산 편리를 위해 저항으로만 구성되어 있다고 가정(상수)
귀환계수=베타=상수로 봄
A가 안정하다고 가정
문제는 베타를 가지고 피드백을 걸면 Af=A(s)/1+베타A(s) > 불안정해짐(베타의해). stability문제가 걸림
안정한 애를 피드백 걸면 불안정해질 수 있음> 안정한진 안한지 따져줘야함.

1.안전 여부
2.안전 수치화
(마진이 얼만큼 이상 있어사 사용할 수 있음)
불안정하면 주파수 보상을 통해 안정화시켜야함
오늘 pspice+matlap이용할 예정>회로+bold plot(손으로 그리는거 나올예정)
안정 정의
BIBO
marginally stable은 임계 안정으로 뒤에서 불안정 판별에서 발진조건 이상 부터 불안정이라 판별함.
LTI system
-선형:중첩+scaling
-시불편:시간과 관계 없이 결과가 동일
어떤 system의 특성을 반영하는 전달함수h(t)를 이용해서 출력이 어떻게 나오는지 파악해야함.
시간 영역에서 전달함수가 있을때 시간영역의 출력이 convolution의 적분형태로 나옴>계산 졸라 힘듦
>주파수 영역에서 계산 전달함수가 있을때 입력이 들어가면 곱셈으로 계산되어 출력나옴.
시간영역의 입력,전달함수를 주파수 도메인으로 보내는 방법:라플라스
주파수의 결과를 다시 시간영역의 결과를 가져옴:역라플라스
전달함수의 안정여부를 확인할때 impulse함수 입력하면 출력이 전달함수로 나옴>안정성을 판별
시간영역에서 전달함수의 특성이 그대로 나오니까
임펄스 함수 구현하는 방법 없음(불가능)- pspice로 Vimpulse 이용해서 억지로 setting가능그러나 실제로는 impulse 반응 대신에 unit step function을 impulse 대신 넣음>?왜 이용 t=0부분에서 impulse와 비슷한 역할음. 불안정한 시스템은 발산안정한 시스템은 수렴실제로는 step함수로 안정성 판단함.
matlap에서는 impluse 함수가 존재함

복소수 도메인에서 H(s)의 pole 위치에 따라 안정성 판별할 수 있음
허수부분 부호가 다른 켤레로 pole이 존재함.

sigma= -500이면 수렴하도록 바뀜
sigma= 0이면 발진


극점의 위치를 따라가면서 그래프로 만들어보자=근궤적도
1)pole한개인 A증폭기를 베타 음성 피드백시 극점이 왼쪽으로 가니까 피드백 걸면 무조건 안정해짐>안정도 검사 필요x
2)pole 2개 베타 피드백 걸면 점점 가운대로 모이다 갈라짐(spilt) 90도 갈라지니까 베타가 커져도 pole이 좌반에 존재함으로 이론적으로 안정함.>실제로는 써먹지 못하는 안정상태가 될 수있음
3)극점이 3개이상이면 문제 발생.
제일 먼 극점 더 멀어짐
두 극점이 만나서 오른쪽으로 감> 넘어가기 직전까지가 안정(그까지 𝜷 를 쓸 수 있음)
허수축을 지나가는 지점의 𝜷 값= 𝜷cr= 𝜷critical
안정한 system이 되려면 𝜷 < 𝜷 cr이어야함.
안정 불안정의 기준이 발진이 된다.
귀환 시스템의 안정도

-발진상황
외부의 별도 입력이 되지 않음
피드백이 걸려있어야함 가능
+xf라면
xf=베타X0
x0= 𝜷𝑨 X0 루푸를 돌고 나와도 동일하게 sin파형이 나와야 일정한 출력이 나오는 상황이 됨.
발진조건(일반적인 기준)
1)크기 동일=loop이득 크기=1
2)phase동일(위상)차이가 0 , 360도가 되어야함.
피드백 증폭기만드는 과정에서 안정여부 따질때
피드백으로 -xf를 걸려있는 상황에서 발진
1)루푸이득 1
2)위상 +_180조건이 된다.
>루푸 이득크기와 위상으로 안정 불안정으로 따질 수 있음
두 조건 동시 만족시 불안정> 발진
안정하려면 동시 두조건 만족 안 하면된다.
1개 만족시 다른 하나를 확인해보면 된다.
w1 (f1)루프이득 1을 만족한 주파수>위상을 확인 180이면 발진(불안정) 다르면 (안정)
w180(f180) 위상 180을 만족한 주파수 >이득 크기 확인 1이면 발진(불안정) 1보다 크면(발산,불안정) 1보다 작으면(수렴,안정)

루프이득 찾기
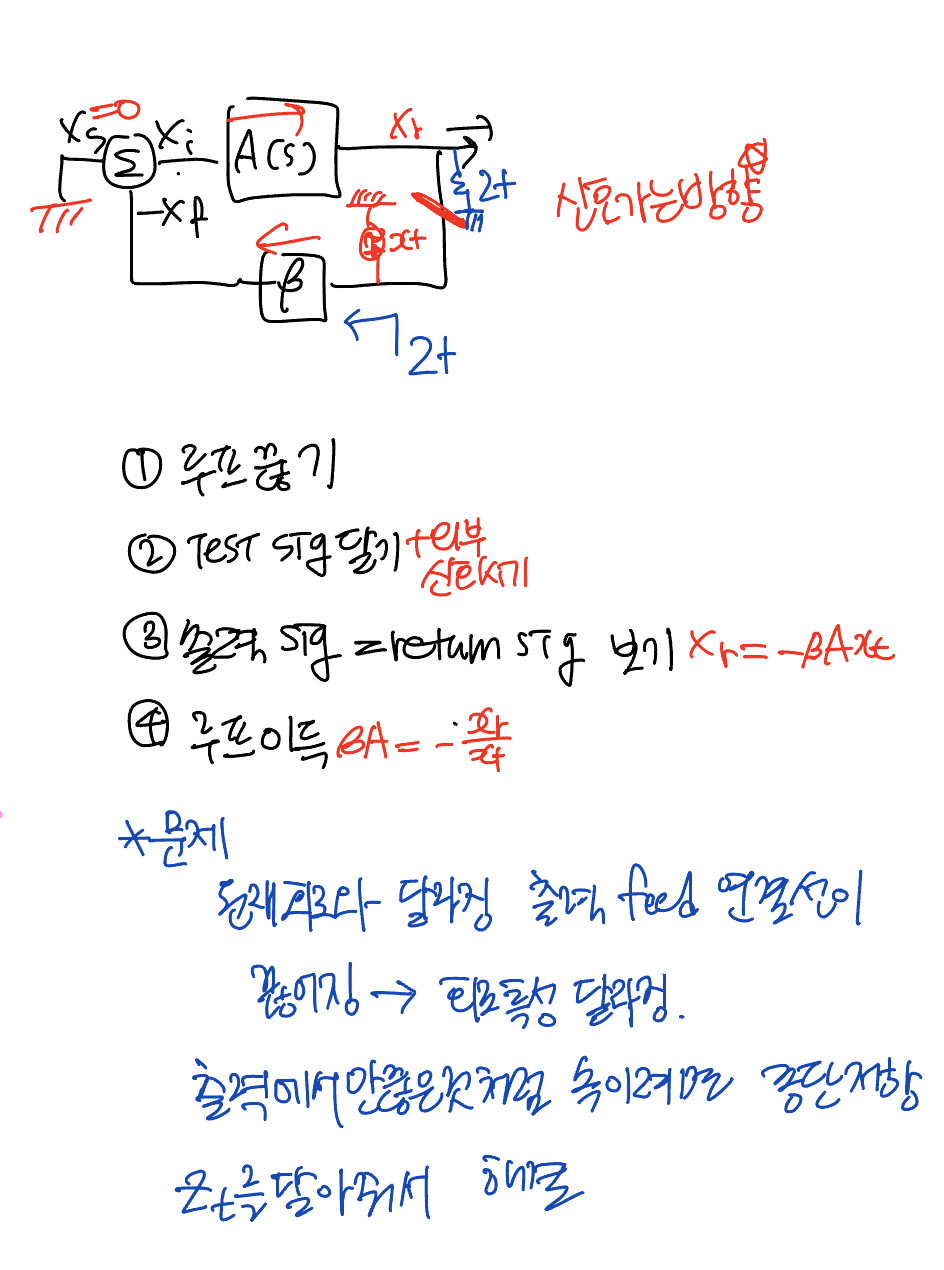

무한대 저항이 보이는 곳에서 끊어서 zt를 안달아줘도 된다.

아이패드에 풀이 작성

보드플랏 안정도 판별
20log }𝜷𝑨(𝒔)|( =0 > 𝜷𝑨 =1
w180에서(위상 180) gain 0보다 작음>루프 이득이 1보다 작음=안정 gain>1:발산 불안정
안정한걸 알겠다.그럼 얼만큼 안정한데
안정한 포인트와 불안정한 지점 차이=GM=0-20log|베타Ajw180|[dB]>0
w1(이득1) 그때의 위상 180보다 낮으면>불안정: 180을 지나가게 되는데 그때 이득이 1보다 큼으로 불안정하게 됨
그냥 180자체를 안지나가야함. 180보다 작아야 안정
𝑷𝑴 > 𝟎 & 𝑮𝑴 > 𝟎 ⟺ 𝝎𝟏 < 𝝎𝟏𝟖𝟎
얼만큼 안정
180까지의 차이=PM=위상 𝜷𝑨 (jw)-(-180) [degree]
보통 하나만 봄 PM>0이면 안정하다고 봄(이론적)
pm>0이라도 pm이 작으면 쓰지 못하는 안정이 된다. (ripple이 졸라많아서 쓰지 못함)
얼만큼 되어야 써먹음? 세드라:적어도 45도 이상 실무적:55도 이상
pm너무 커도 쓸 수 없음 신호가 늘어져서 사용x 고속으로 동작회로의 경우x

실제회로에서 𝜷𝑨 찾기 어려움
그럼 더 쉽게 찾는 방법 없나
루프이득 보드 플랏을 구하는게 아니고 이미 주어진 A증폭기 보드플랏을 그려서 안정도 판별하기
( 𝜷가 상수니까)𝜷𝑨위상 그래프와 𝑨위상 그래프가 차이가 없음 > w1(f1)가 1이되는 지점
𝟐𝟎 log𝟏𝟎 𝜷𝑨(𝒋𝝎𝟏𝟖𝟎) [dB]=0 일때
20 log10 𝐴(𝑠)𝛽 = 20 log10 𝐴(𝑠) − 20 log10 (1/ 𝛽)=0 인지점의 주파수를 찾으면 w1을 구할 수 있음
20 log10 𝐴(𝑠) = 20 log10 (1/ 𝛽) 주파수와 관련없고 𝛽관련해서 수평한 그래프가 그려짐
두 그래프가 교차하는 지점이 w1이 된다.>이때의 위상이 180도임>불안정,발진
두 교점이 두번째 pole에서 만난다면
pole이 10배이상씩 떨어져있다면.
1번째 pole에서 위상이 -45도
2번째 pole에서 위상이 -135도(PM이 45도가 나옴)
3번째 pole에서 위상이 -225도
>>이부분 복습하기

보상
pm<0이거나 작을때
어디에다 보상? A에다가 해줌
커패시터의 시정수를 찾아서 시정수의 역수가 극점찾음
극점2개.. 독립적으로 존재하는 커패시터가 2개 존재

'3-2학기 > 전자회로설계' 카테고리의 다른 글
| 20241203 13장 clock _generators & 555 timer Ic (0) | 2024.12.03 |
|---|---|
| 20241126 Current Monitor(11장) Voltage Regulator and OP-AMP Applications(12장) (2) | 2024.11.26 |
| 전자회로설계 파일 (0) | 2024.10.05 |


