알쏭달쏭 공부한거 쓰기
10/31 Lecture 7_Qunantum theory ofo the Hydrogen Atom 본문

chapter 4의 원자 모델을 이어서 배울 예정
기존의 보어 모델까지 배움.
보어 모델이 가진 한계가 있어서 다음 챕터의 슈뢰딩거 방정식을 배웠고 , 그 개념을 도입해서 보어 원자 모델의 한계를 극복한 새로운 이론임.
양자 이론=슈뢰딩거 방정식을 말함.
입자나 박스 처럼 눈에 보이지 않는 세상의 입자의 행동을 설명하는 법칙이 슈뢰딩거임(고전 역학에서는 뉴턴 법칙)
이 슈뢰딩거 방정식을 이용해서 전자를 설명하고자 함.
새 개념이 나오면 항상 먼저 쉬운 것을 적용해서 confirm하는것임.
원자번호 1번에 해당하는 전자1개를 가진 수소 원자에 대해서 이 이론을 적용해서 결과를 확인해볼 것임.
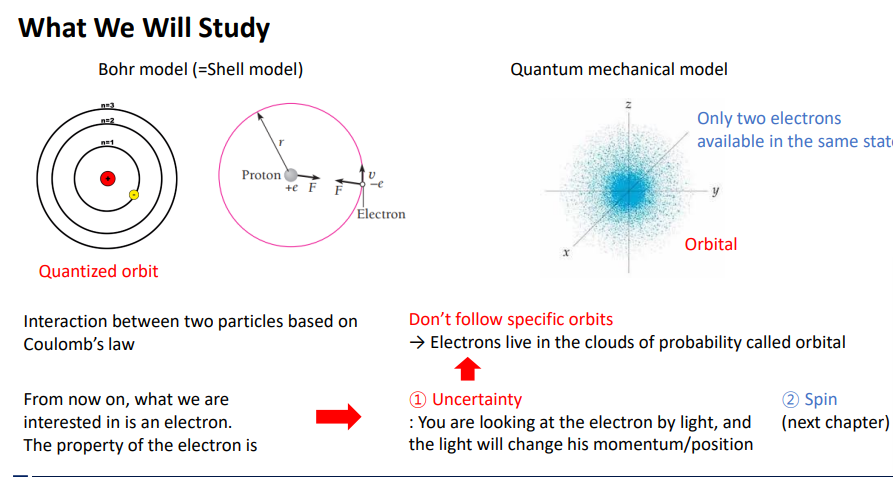
왼쪽의 사진은 새로운 형태의 원자 모델
원자 핵이 1개 센터에 존재
가에 각각의 포인트가 전자가 발견될 수 있는 확률 밀도라는 개념으로 표현되어 있음.
진짜 원자가 어떻게 생겼는지를 파악하는 챕터
이번 챕터에서 배울 내용
1.보어 모델의 문제 >해결하는 방법 (슈뢰딩거 방정식을 도입) 양자 역학이 적용된 모델이라고 해서 양자역학모델이라고 부름,다른 말로 슈뢰딩거 구름 모델
보어와의 차이점은 전자가 특정 궤도를 가지고 있는게 아니라 양자 역학에서 배운 내용으로 전자가 발견될 위치는 확률로서 프사이 제곱으로의 의미를 가지고 있다.
전자가 발견될 확률이 높다 낮다 정도만 말할 수 있다.
우리가 할 수 있는건 확률적 개념으로만 말 할 수 있다.
2. 이런 전자의 위치를 말하는 과정에서 양자 넘버가 나온다 .
보어 모델의 n에 이름을 붙여줌.
기존의 n외의 필요한 것들 l, mi을 설명함. > lm이 있어야 모델을 설명할 수 있음=보어 모델에는 lm이 없어서 문제가 있다고 생각 할 수 있음.
3.zeemam 효과
-ideal to non ideal
-원자 스펙트럼 라
이번시간에는 계속 보어 모델의 한계에 대해서 이야기함.
보어 모델의 실험적 증거는 스펙트럼. 빛이 흡수 ,방출시 라인으로 보여짐.
예를들어 빨간색이 나오는 파장이 300nm라면 n=1에서 n=2로 에너지 전이가 발생할 때 필요한 에너지와 동일해서 300nm가 나온다라고 해서 보어 모델의 증거가 되었는데, 이게 문제가 있음.
라인이 1줄만 보여야하는데, 실제 경우에는 여러개의 라인이 있음.
왜 일어나는지 설명하기 위해 zeeman 효과를 설명함.
매 챕터마다 이상, 비이상적인 케이스가 나옴 .
이 수업이 끝나면 이제 보어, 슈뢰딩거 듣지 않음.
?이런걸 배우는 이유
이상, 비이상.
대학생활에서 배운걸 보면 이상적인 것을 배움> 실제 적용된 사례에서 무엇이 다른지를 깨닫는 사고방식을 익히는 과정임.
회사에 가셔도 동일한 접근 > task.가 주어지면, 현재의 상황.
지금까지 해오던 모델이 무엇이며 어떤 문제가 있어서 어떤 것을 도입하며 문제를 해결해나가는지를 학부 과정에서 다양한 과목을 통해 배우는 것임
항상 이상적인 이론과 실제 케이스를 비교해보길 바람

보어의 문제점을 볼 예정- 보어 모델에서 수소의 스펙트럼만을 다루어 봤음. 보어 모델에서는 오직 수소만 설명할 수 있었음. >다른 원자를 설명하기 위해서 다른 원자 모델이 필요했음(동기)
해결하는 방법: 전자에 관심이 있으니 wave function을 도입한 , 입자의 양자 행위인 슈뢰딩거 방정식을 통해서 모델을 세우자는 것에서 시작.
입자나 박스에서 L이라는 1D가 아닌. 3D 핵이 센터에 있고 전자가 도는 구형태로 볼 예정.
그렇기 위해서 기존과 달리 새 좌표계가 필요함.
필연적으로 새 좌표계를 풀기위해서 나오는 n ,l,m 상수가 나오고 양자 넘버라고 지칭할 것임.
-수학적 유도
-물리적의미
-왜 n,ㅣ,m이름을 가지게 되었는지.
전자의 정확한 움직임을 알 수 있음.
에너지와 모멘텀을 얼만큼 가지고 있고
지만 effect
-여러 제약이 더해짐 : 자기장 적용시에 모델 확인
회전과 위치를 불확정성 원리로 고려할 수 있게 된다.
무얼 위해 이걸 하는가.
보어 모델은 핵이 하나 있고 전자가 궤도를 돈다.
중간고사에서
전자가 어떻게 당기는 힘에 끌려서 충돌하지 않고 왜 이 특정 위치만 , 이 반지름만큼 떨어진 공간에 존재할 수 있는가 .
드브로이 아이디어로 n=1,n=2 특정 궤도에만 전자가 안정하게 존재할 수 있다.
+,- 관계 두 입자를 살펴보니, 특정 궤도가 양자화 되어 있다. 모든 반지름이 아니라 특정 반지름 사이즈를 가지는 곳에서만 전자가 존재할 수 있다.
전자에 계속 집중.
전자가 어느 궤도만 가는 것은 알겠고
그 전자가 가지는 특징이 무엇이 있는지 알아보자 .
전자의 양자 입자가 가지는 성질은 불확정성임
무언가를 관찰할 때 모멘텀과 위치를 동시에 정확하게 관찰 할 수 없다는 원리가 적용됨,
이것을 위해서 챕터1에서 상대성 이론이 나옴.
빛이란 것을 이해해야 빛이 파장임을 이용해서 드브로이에게 가서 빛이 파장 특성도 가지고 있고, 입자특성도 가지고 있다면, 모든 물체가 입자, 파동 성질을 가진다. (이중성)>전자와 같은 입자를 파동으로 설명하기 위해서 wave packet이 나옴.
>wave packet 구성하다 보니 모멘텀과, 위치를 둘다 정확히 파악할 수 없는 불확정성 원리가 나옴.
이 불확정성 원리를 보어 모델에 적용하면.
전자가 특정 궤도에 있다는 사실을 말할 수 없음 .
왜냐하면 특정 궤도라는 것이 불확정성을 위배함. > 전자가 양자화된 궤도를 따라가는 것으로 설명하지 못함
그래서 나오게 된게 새로운 양자 모델이라고 해서 궤도라고 하지 않고 오비탈이라는 개념이 나오게 되었음.
오비탈은 전자가 궤도를 돈다라는 것이 아니라 살고 있다라는 의미
전자가 오비탈이라 불리는 확률로 되어있는 구름/집/공간에 살고 있다라고 표현함.
라인으로 표현되는 것이 아니라 있거나 없다는 오비탈 컨셉으로 원자의 모델을 설명함.
+
1가지 더 전자의 특성(스핀)을 고려해야 원자 모델을 설명할 수 있음(다음 챕터)
spin을 통해서 오비탈 외의 전자가 한 state에 두개만 존재할 수 있다는 파울리 베타 원리가 나오게 되었음.
*이번 챕터
왜 보어 모델에서 양자역학모델로 바뀌게 되었는지 배움
*다음 챕터에서는
이 공간에 전자가 몇개 있기 때문에 무엇이 달라지게 되는지를 배울 예

가장 간단한 전자1개인 수소원자의 경우에 슈뢰딩거 방정식으로 적용해봄.
지난시간에는 슈뢰딩거 방정식에 박스, 입자, 포텐셜 well을 다룸 이번에는 원자에 적용.
더이상 1D simple이 아닌 슈뢰딩거 x하나만 다루는게 아니라 x,y,z인 3차원을 다룸.
다른 좌표를 고려해서 풀어보려고함.
proton은 가만히 있고, 전자가 움직이는 것을 고려
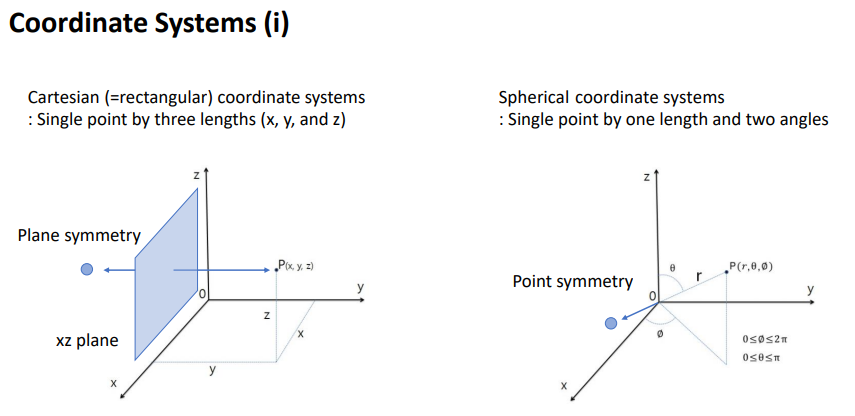
새로운 좌표계가 필요함.
기존 좌표계는 직각 좌표계로 설명해옴.
3가지 길이를 이용해서 한 지점을 설명함.
>면 대칭일때 사용하면 좋음.
x,z plane에 대비해서 p가 한쪽 축만 달라졌을 때에 좋음
이번에는 구 좌표계를 써야함.
1가지 길이와 2개의 각을 이용해서 한 지점을 설명함.
센터에 핵이 있고 전자가 주변에 도는 원자 구조에 적합한.
>원점을 기준으로 대칭을 설명할 때 유용함.
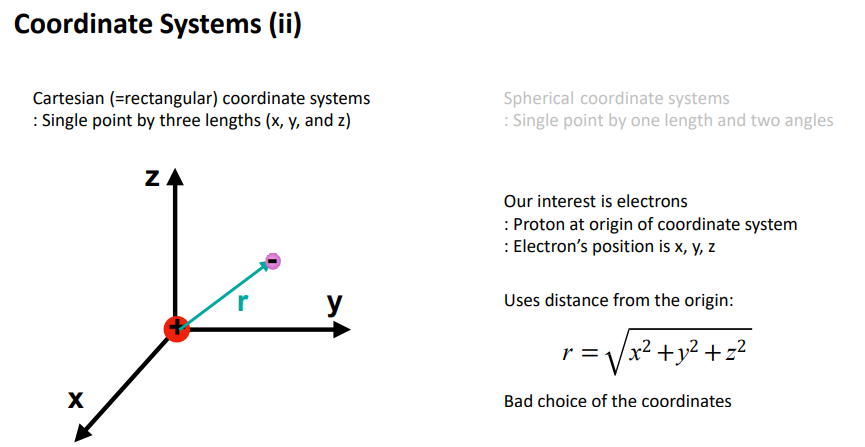
기존의 직각 좌표계에서 구에서의 하나의 길이 표현
원점에 핵을 둠.
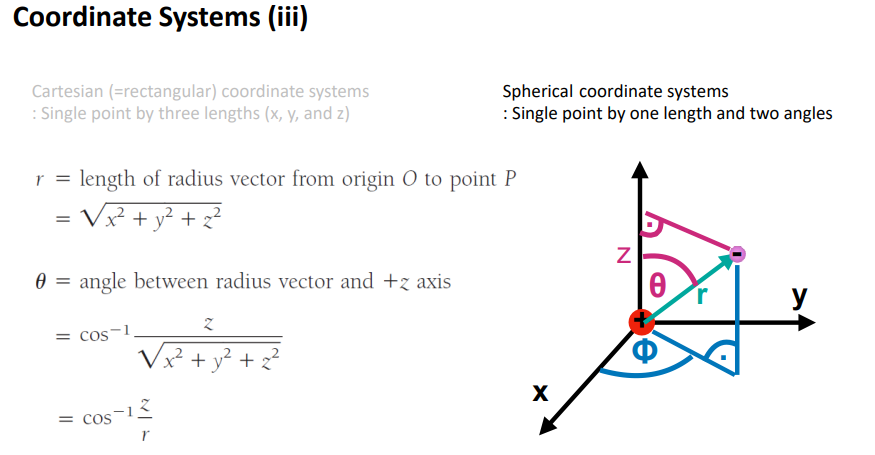
세타가 얼마인지도 직각 좌표계와 구 좌표계의 변환

슈뢰딩거 방정식을 3D직각 좌표계를 구좌표계로 바꿈.
여기서 프사이 wave function을구해야함.=전자가 존재할 수 있는 확률이니까
박스 안에/ 수소 원자안에 전자가 어디에 존재할까에 대해서 알아야함.
슈레딩거 방정식에서 필요한 파라미터는 total E아니고 KE도 아닌 어떤 포텐셜이 주어진 상황인가.
U가 중요함.
이전에 ideal infintie potential well> fintie well> Thin fintie> Harmonic oscillator 다룸.
이번 경우에는 쿨롱 힘을 받는 포텐셜을 이용함.
거리에 반비례 전하의 제곱, 잡혀있으니 음수
수식을 변형. r^2 sin세타 모든 항에 곱함.
wave funtion을 길이와 두개의 각으로 표현함.

그 수식을 가져옴.
그럼에 이렇게 만든 이유 구좌표계가 하나의 길이, 두개의 각으로 표현된 wave function이 길이, 파이, 세타로 해당하는 방정식으로 독립적으로 표현할 수 있음.
프사이의 파라미터가 서로 서로 독립적인 항으로 표현> 수학적으로 powerful함.
슈레딩거 방정식에 가장 많이 하는게 미분, 2번 미분하고 이렇는데, r에 대해서 미분할 때 다른 2개의 파라미터는 r과 관려이 없으니, 상수처리할 수 있다는 것임
수식 상수에 R세타파이들이 나누어줌. >각 항과 관련된 term만 남게
이렇게 항을 정리한 이유
첫번쨰 항은 세타, R으로 표현
두번째 항은 세타 항만으로 표현
세번째 항은 파이에 대한 함수
네번째 항은 r과 세타에 대한 함수로 표현

끼리끼리 뭉쳐봄. 파이만 넘기고 r,세타 항만 나둠.
수식이 의미하는 것을 파악하기 위해서 수학적 도구가 필요함.
f(r,세타)=g(파이(세타,r관련x))
두 함수가 같아질려면. 수학적으로 두개가 상수여함.
왼쪽의 세개항 더함, 오른쪽 항이 상수여야함.
오른쪽 파이로만 해당하는 항이 상수로만 표현> 상수 mi^2으로 나타남.
새로운 양자 넘버라고 지칭함.

기존의 3D, 구좌표계로 바꾸어서 항 정리하는 과정임.
sin제곱을 나눔. 두번째 항이 오른쪽으로 넘어감. 기존의 오른항은 상수로 표현.
그 이유는 왼쪽한 r대한 항, 오른쪽은 세타에 대한 항> 방정식으로 되어 있으니, 각각의 함수가 동일한 상수여야함.
이번에는 l(1+ㅣ)이라고 표현함.
마지막으로 .왼쪽의 항 그대로 두고 이것을 상수로 표현.
오른 항도 왼쪽과 같으려면 동일한 상수가 되어야함.
방정식이 두개가 나옴.
3개의 방정식이 다시 주어짐
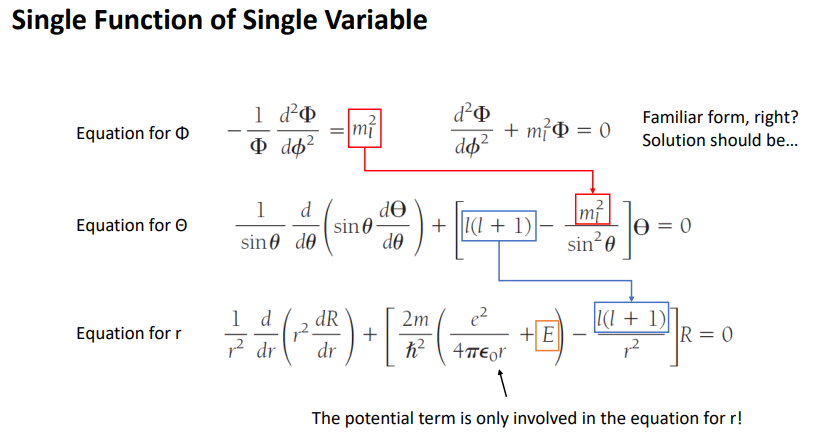
지금은 하나의 변수로만 각각의 함수가 구성되어 있음.
각각의 상수가 각 방정식에 연결되어 있음.
우리가 해야하는건 이 상수가 무엇인지 알아야함.
상수가 연결되어 있다는건 경계 조건이 엮여있다는 의미
E> l결정> m결정
첫번째 수식에서 -을 넘기고 본인을 두번 미분하고, 본인을 배수해서 더하면 0이다라는 방정식이 생김.
이 함수에 대한 sol을 우리가 알고 있음.
마지막 거리에 대한 방정식으로 표현된 식만 포텐셜과 관련이 있음 나머지는 관련이 없음.
수소원자의 핵이 전자를 쿨롱 힘으로 당기고 있는 상황에서의 전자의 위치를 파악하고 싶은데 세타랑 파이는 포텐셜과 관련이 없는데 r에 대해서만 포텐셜과 관련이 있다.

3개의 eq 중 1번째 방정식의 의미 ml의 의미를 알고 싶음. 그 조건 찾는 중
2차 미분방정식의 해의 꼴이 exp꼴로 표현된다.
파이가 얼마인가에 결정된다.
그렇기 위해서 양수에 파이 만큼 떨어져 잇는 경우.
한바퀴돌려도 같은 값을 가져야함. (파이의 정의에 의해서 설명된다)
파이가 0일때는 1이된다.
파이가exp 2ㅠml일떄도 1이되어야한다.
해가 exp이니까.
그래서 mi=0부터 시작함.
1번을 오른쪽으로 돌리거나, 왼쪽으로 돌리거나.
바퀴인 2ㅠ * 정수배이기만 하면된다.
따라서 m은 +-(방향) 정수배(바퀴 횟수)만 가질 수 있음-0은 0바퀴
물리적 의미 보다는 어떤 값을 갖는지, 어디서 파생되었는지 파악하면 된다.
마그네틱 양자 넘버라고 불린다. > 이름이 m임
이 이름인 이유는 다음시간에 배움.
m이 가질 수 있는 max이 무엇인지 생각하려면
아까 3개의 방정식이 상수가 연결되어 있음 경계조건으로 연결되어 있음.
subL은 무엇인가지 알려면, 2번째 수식이 필요함.
l: 오비탈 양자 넘버
이 수식을 풀면 ml의 경계조건이 +-l이 된다. >수학적으로 +-l까지인걸 풀진 않음.
여기서 중요한 건 m이 왜 0과 +,-값을 갖는지가 중요함.
ㅣ이 왜 오비탈 퀀텀 넘버인지는 다음시간에 할 예정.
오비탈 퀀텀 넘버의 이름 이유를 알려면 3번째 방정식을 풀어야함. ? 3번째는 또 푸네;2?

E1 찾기, Eq에 n=1, l=0인 wave function R을 넣어서
정의된 R,n,l을 대입 미래 계산된 것을 씀.
R를 r로 미분된것과, 그 값을 r^2을 곱한걸 다시 r로 미분 된 값을 그대로 가져와서 봄

ㅣ=0이니 없어짐.
준 값을 대입해서 다시 정리.
2번째 항부터 달라짐. E1해당하는 항*R이 2항으로 옴.
m인 항이 3번째 항으로
마지막 항이 아까 안 쓴 항이 옴
1/r로 정리하려고 이렇게 씀.
중요한 건 이 수식이 가지는 의미를 파악하는게 중요함.
최종적으로 얻은 방정식의 모습은 뭐 더하기 뭐 곱하기 뭐하면 일단 =0의 꼴임
0이 되려면 각 항이 0이 되어야함.
파란색 항, 녹생 항이 0이어야함. a0로 정리 .
a0는 n=1일때의 반지름=보어 반지름을 뜻함.
반지름 한개 알아냄. (아까 dr로 미분한 항으로 바꾸면서 생김)
E1에 대한 값을 알아냄. -a0값 대입하면 값을 알 수 있음. a0제곱에 반비례한 상태
문제에서 E1구하라고 함. E1구함
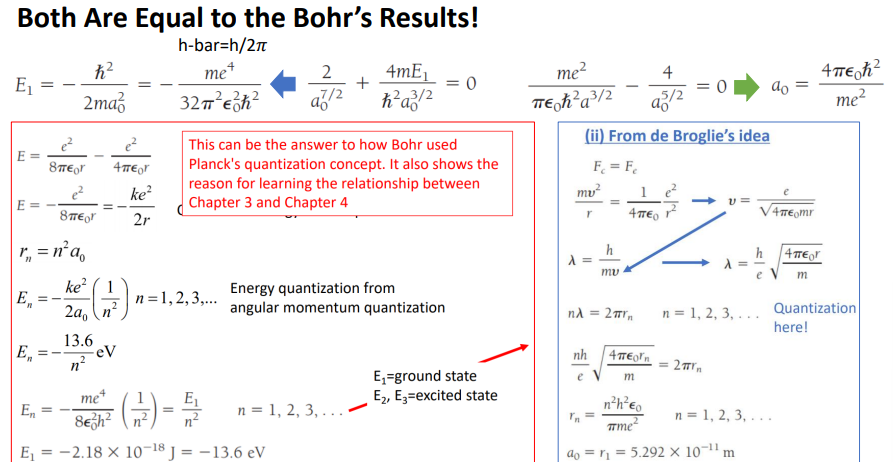
이 수식에서 E가 가지는 중요한 의미
다시 보어 모델로 돌아감.
보어 모델이 갖고 있는 힘.
보어 반지름을 계산하기 위해서 왜 정상파를이용 아이디어 2개 도입해서 전자가 특정 위치에만 존재할 수있는 것을 파악.
힘두개 >v>파장길>파장길이 원둘레여야함인 드브로이 아이디어를 도입해서 양자화를 도입함 .>모든 r이 아니라 n제곱에 비례한 r만 가질 수 있음.
보어는 슈뢰딩거 방정식 양자 역학 상수를 도입하지 않았지만 r이 얼마인지 도입해서 푼 값과 굉장히 유사함.
n=1일 넣은 값이 .동일함.
엄청난.. 1이 발생.
보어가 양자역학의 숫자를 쓰지 않고도 양자역학에서 얻은 반지름과 동일하게 얻음
에너지 텀을 보면. 모든 r에 대해서 모든 E를 갖는게 아니고 특정 r에 대해서 특정 E만 가짐 n^2반비례
슈뢰딩거 방정식으로 푼것과 동일함.
보어의 개념이 맞았다. 슈뢰딩거 방정식으로 푼것도 전자의 모델을 잘 설명함.
양자 역학이 맞다.

[정리]수학적으로 구좌표계로 슈뢰딩거 방정식을 표현하니 방정식을 맞추기 위해 상수 도입.
ml, l(1+l)이라는 이름을 줌
이름을 붙임. 보어 할 때는 n=1이라고 했는데
슈뢰딩거는 n는 정수배로 양자화 양자역학에도 맞아 떨어짐.
1---무한대>>무한대로 가면 고전 역학으로 설명해도 맞아 떨어지는 correspond princple까지 확장된다.
다른 두가지 추가적인 양자 숫자가 필요함. (수학적으로)
l=1...n-1
mi=0,+-1,,...+-l까지

왜 이름이 오비탈인가. origin을 파악하기 위해서 다시 방정식을 봄
l이 해석하기 명확하지 않음.
해석하기 위해서 파장 함수 3가지 중에 R에 해당하는 것만 다시 보자 3번째 방정식
이 방정식은 오로지 전자의 거리에 대한 motion에만 판단할 수 있음.
핵이 원점으로 부터 멀어지느냐, 가까워지느냐만 관련.
문제는: 수식에 총 에너지가 있음. 그게 왜 문제>? 총 에너지는 전자의 KE운동에너지를 가지고 있음.
radial motion과 관련이 없는 orbital motion의 KE를 총에너지가 포함함.
radial 전자가 핵으로부터 멀지, 가까운지 정도만 나타내는데 운동에너지는 전자가 도는 회전하는 모습을 나타냄.
이 두 motion이 관련이 없음.
두 motion의 방향이 다름.
오비탈 모션. 정해진 r에 대해서 얼만큼의 에너지로 (속도)로 도는지를 E가 포함하고 있음
근데 radial과 관련이 없는데 어떻게 해석?
E안에는 radial, orbital KE를 포함 이 오비탈은 R과 관련이 없는데 , 어떻게 설명하느냐가 문제인데
>KE를 두 에너지로 나눔.

수학적으로 해석.
KE이가 두개의 부분으로 나뉘어져 있음.
거리에 해당하는것과 도는 것으로 해당하는 것으로
알고보면 거리에 따라 움직이는 힘과 궤도를 따라 움직이는 힘 2개의 운동에너지를 가짐.
U는 쿨롱 힘만 작용.
그 total energy를 3번째 E에 넣음.
포텐셜을 날라감.
오직 radial과 orbital KE 로만 표현된다.
이 방정식은 오직 R에 대한 함수로만 표현되어야하는데 orbital KE,와 상수는 R과 관련이 없음.
수학적으로 거리와 상관없는 파라미터를 지우려면 두개의 값이 같아서 상쇄되면 된다.
그래서 KE오비탈=l에 대한 수식으로 정리됨.
KE오비탈은 1/2mv^2로 정리된다.
m질량의 물체가 v라는 속도로 직선 운동을 하면 =p로 설명
혹은 mvr m라는 물체가 v라는 속도를 r이라는 원운동을하면 =L (각운동으로 표현)
KE를 L로 표현할 수 있음.
L로 표현한 KE를 l대한 수식으로 정리할 수 있음.
l의 의미: 전자가 어떤 궤도에서 움직일 수 있는 각운동의 크기를 나타냄.
결국 각운동은 돌기때문에 발생하는 모멘텀.
l은 오비탈과 관련있음.
무언가 도니까 힘을 만들어냄 그래서 l을 오비탈 퀀텀 넘버라고 불려지게 된 것임.
l이 특정 값만 가짐. 1..n-1
여기서 중요한 것은 l이 왜 오비탈 이름이 붙여진 것이 중요함(KE orbital과의 관계성에 대해 설명하면 된다. )

오비탈 퀀텀 넘버는 전자의 각운동의 크기를 결정한다 l > L을 알 수 있음.
L은 양자화 되어 있다.
고전 역학에서는 어느 값이나 가질 수 있었음. mvr에서 모든 r에 대해서 가능 .
L이 l의 수식을 만족해야함으로 l이 양자화 되어 있으니, L도 양자화 되어 있다.
ex) n=1 l=0 L=0
E1일때는 각운동이 없다
보어 모델에서는 전자가 안정적인 상태에서 궤도를 돈다(항상 움직임 ) 라고 설명했는데 .
실제 경우에는 전자가 가장 낮은 상태에서 각운동을 갖지 못함으로 가장 낮은 상태에서는 전자가 그 장소에 시간을 오래 보냄 즉 거의 움직이지 않음을 나타냄. (특정 에너지 상태에서 돌 수 있는 모멘텀까지 고려함. )
>돌 수 있는 힘/에너지/속도도 양자화 되어 있다.
이것이 보어와의 차이
l을 숫자로도 표현하지만 spdfghi라는 이름으로 오비탈 이름을 붙여줌.
전자 상태를 n, ㅣ상태로 표현함.
n>1 3가지 방정식으로 통해서 경계 조건이 있음.
n=2, l=1인 경우에 2p state로 불림
> 오비탈 퀀텀 넘버에서 나오게 됨.
> 슈뢰딩거 방정식을 구좌표계로 바꾸니 이렇게 나옴
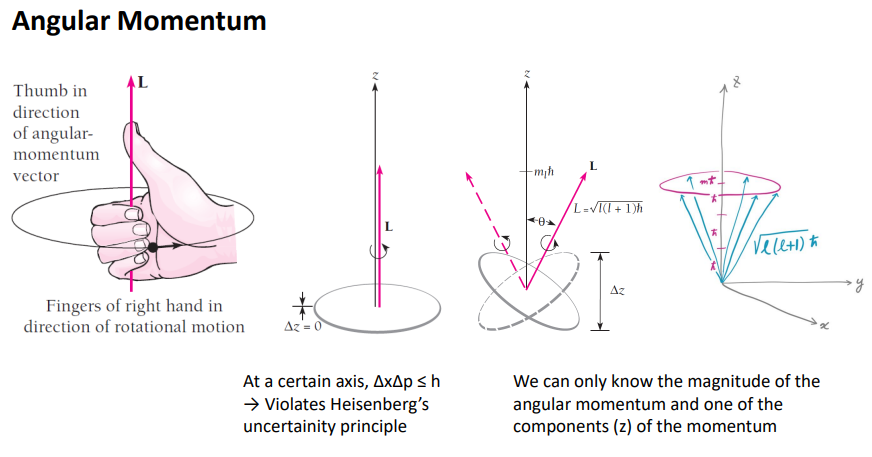
마지막 concept
오비탈 이름이 왜 붙여 졌는지 알아봄.
오비탈이 만들어 내는 건 전자가 어디서 돌면 엄지손가락 방향으로 모멘텀을 만들어냄.
무언가 돌면 엄지손가람 방향으로 각운동이 정의된다.
전자가 궤도를 돌면. l이 몇이면, L이 정의 된다.
돌기만 하면. L이 만들어짐.
여기서 양자 역학에서
전자가 돌고 , 우리가 L을 아는 것 자체가 하이젠베르그의 불확정성원리를 위반함.
L이 정의가 되었다는 것은 전자가 저 평면에서 도는 것을 확정하게 된다 .
만약 전자가 도는 궤도의 평면을 모르면 각운동량이 위쪽으로 생성된 것을 모를텐데 . 현재 z축으로 L이 생겼기 때문에 전자는 이렇게 돈다는 위치를 정확히 알게 된다.
이 뜻은 z축으로 해당하는 편차가 존재하지 않는다는 것. 따라서 불확정성의 원리가 깨짐.
이것을 막기 위해 전자는 고정된 평평한 원반을 도는 것이 아니라 z축으로 편차를 가지면서 팽이처럼 돌것임.
그에 따라 L이 방향이 왔다갔다 할 것임
크기는 수식으로 정해져있음.
L정확한 위치를 평가할 수 없음 by 불확정성 원리
그럼 우리가 알 수 있는건 얼만큼 변형될 수 있는가를 알아야함.
그래서 그떄 필요한 것이 ml이라는 마그네틱 퀀텀넘버라고 불리 상수가 필요함.
다음시간에 왜 ml이라는 마그네틱이 붙여지는지 배울건지
이번에는 오비탈 퀀텀넘버가 첨자로 붙었는지 배울 예정, l이 오비탈 퀀텀 넘버면 오비탈과 관련있는데,
ml이 무슨 의미를 가지는지.
ml도 양자화 되어 있음. 따라서 L이 가질 수 있는 크기가 양자화 되어 있음. 병형되는 정도를 알 수 있음.
L이 돌수 있는 영역도 양자화 되어 있음.
오른쪽 그림 처럼 팽이처럼 도는데 주어진 각운동에 대해서 특정 각도이내에 선택적으로 가능함.
L이 l에 의해 결정된다. L의 길이를 z축으로 투영시 그 값이 원점에서 양자화(m)된 값만 허용된다.
이부분... 짱 자세히 설명하시노..
안 되는 경우
L 의 길이가 양자화된 l일지라도 z축에 투영했을 때의 길이가 1.5h처럼 나오면 ml이 양자화되지 않으므로 L이 해당 방향으로 각도를 가질 수 없음.

l은 오비탈 퀀텀 넘버는 전자의 각운동 모멘텀의 크기를 결정한다.
마크네틱 퀀텀 넙너는 각운동 모멘텀의 z성분을 결정한다. >L모멘텀의 orientation을 ,각도를 결정함. (공간 양자화 )
두 조건을 다 만족하려면, 오른쪽 그림의 노란색의 부분 전자가 발견될 수 있음.
특정 각도의 L은 space의 양자화를 보여줌.
불확정성 원리에 의해 나오는 상태
z축만 알려져있음.
xy는 잘 몰르는 상태가 되므로 불확정성 원리를 위배하지 않고 설명할 수 있음.

슈뢰딩거 방정식으로 도입해서 반지름과 에너지가 보어 모델에서 제시한 값과 일치
그때는 무시한 에너지의 몇 배 비례한다 했던 n이 양자역학에 와서는 principal quantu number이라는 이름을 받음.
n의 의미
보어: 전자가 n에 해당하는 지점에 있다라고 했다면
양자 역학에서> 전자가 발견될 수 있는 확률, 영역 사이즈를 결정
n이 작은 핵과 가까운 곳에 뭉쳐서 발견
n이 클수록 먼 곳에서 발견될 확률을 나타냄.
전자가 멀리 있을 수록 쿨롱 힘이 거리에 반비례하므로 잡고 있는 힘이 약하므로 더 쉽게 나갈 수 있음.
보어 때처럼 n만 /거리만으로 생각하면 원자 모델을 충분히 설명하지 못함.
**세번째 전자가 발견될 수 있는 확률이 원형으로 발견되지 않음.
전자가 발견될 영역이 삼각형, 피라미드, 아래에만 발견 등 기괴한 모델을 보어모델이 설명하지 못함(보어의 문제점)
=이 angular momentum이 양자화 되어 있기 때문에 특정 모양을 가짐
모양이 모든 값을 가지고 팽이처럼 도는게 아니라 특정 각도만 가지는 L만 존재해야하기떄문
양자화 되지 않는 각도의 영역에는 전자가 발견될 확률이 0이 되는 거임.
L이 크기와 방향이 양자화 되어 있으므로 ,클라우드/발견될 확률 영역이 양자화 되어 있음.
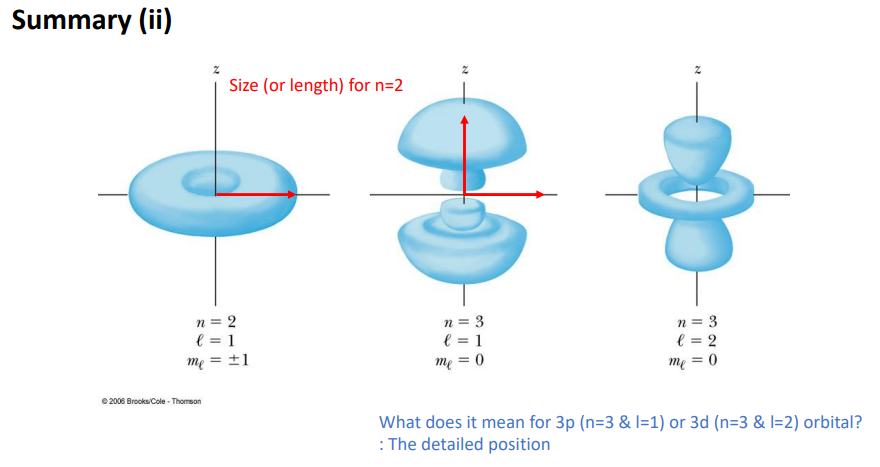
전자가 존재할 확률이 있는 영역이 각기 다름.
다 오비탈을 뜻함.
wave function을 계산해서 제곱한 확률 분포가 저 형태임.
왜 저런 형태인지 설명하기 위해서 새로운 파라미터가 있어야함.
과거 보어 모델은 n에 대해서만 표현했음. n이 갖고 있는 의미로만 위의 영역이 설명이 되지 못함.
ml일단 무시하고 1,2그림 비교하면 n에 대해서 무엇이 달라진지 알 수 있음> n이 커짐 반지름이 커짐.
더 넓은 영역에서 전자가 발견될 수 있는 확률이 존재한다.
양자 역학에서 n은 전자가 발견될 오비탈.확률분포의 사이즈를 결정.
근데 왜 원이 아니냐?
3p,3d오비탈 차이 의미
사이즈가 n=3으로 같은데
전자가 가지고 있는 각운동 모멘텀의 크기가 다를때 l이 다름.
그리고 ml에 따라서 각도.방향이 결정된다.
> 이것 두개를 더 확인하면 디테일한 모습을 결정할 수 있다.
공간의 양자화 개념만 이해하면 된다.
오비탈-원자 속 전자가 양자역학을 이용하여 공간적인 퍼짐으로 나타낸 것 .궤도함수
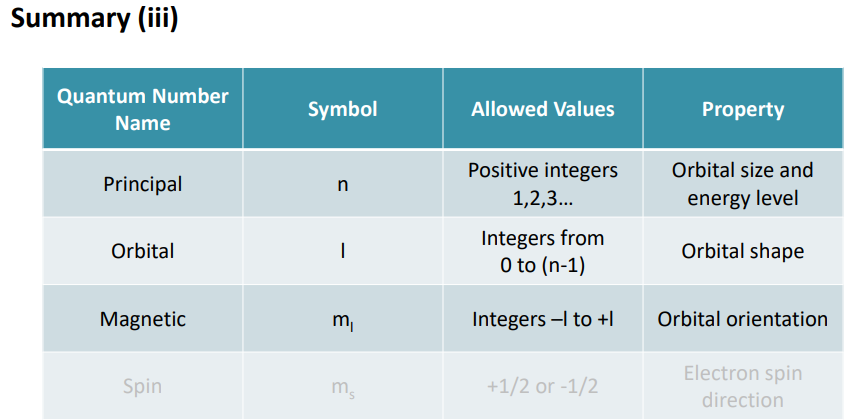
특징이 중요함. 가능한 값
L=각운도의 모멘텀 크기가 가능한 위치량, 전자가 존재할 수 있는 영역이랑 다름 연관은 있지만.
존재하는 영역에 수직으로 L이 서있는 거
다음시간에 원자 모델을 설명하는 한가지더 상수가 있음. 이걸 설명할 예정임
궁금한점
l>m의 경계조건을 만드는 건 수식으로 정립이 된건 알겠는데
n>l의 경계조건을 왜 만들지
'3-2학기 > 현대물리' 카테고리의 다른 글
| 9/3일 현대물리 >lms 영상 (1) | 2024.10.27 |
|---|---|
| Lecture1 현대물리 _overview (0) | 2024.10.20 |
| 10월 17일 현대 물리 (0) | 2024.10.20 |
| 10월 15일 현대물리 (0) | 2024.10.20 |
| 10월 10일 현대물리 (0) | 2024.10.20 |


